本试题 “已知椭圆E:x2a2+y2b2=1(a>b>0)的离心率e=22,在椭圆E上存在A,B两点关于直线l:y=x+1对称.(Ⅰ)现给出下列三个条件:①直线AB恰好经过椭圆E的一个焦点;...” 主要考查您对椭圆的标准方程及图象
椭圆的性质(顶点、范围、对称性、离心率)
圆锥曲线综合
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 椭圆的标准方程及图象
- 椭圆的性质(顶点、范围、对称性、离心率)
- 圆锥曲线综合
椭圆的标准方程:
(1)中心在原点,焦点在x轴上: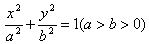 ;
;
(2)中心在原点,焦点在y轴上: 。
。
椭圆的图像:
(1)焦点在x轴: ;
;
(2)焦点在y轴: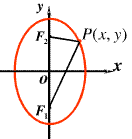 。
。
巧记椭圆标准方程的形式:
①椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
②椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上;
③椭圆的标准方程中,三个参数a,b,c满足a2= b2+ c2;
④由椭圆的标准方程可以求出三个参数a,b,c的值.
待定系数法求椭圆的标准方程:
求椭圆的标准方程常用待定系数法,要恰当地选择方程的形式,如果不能确定焦点的位置,那么有两种方法来解决问题:一是分类讨论,全面考虑问题;二是可把椭圆的方程设为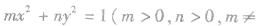 n)用待定系数法求出m,n的值,从而求出标准方程,
n)用待定系数法求出m,n的值,从而求出标准方程,
椭圆的离心率:
椭圆的焦距与长轴长之比叫做椭圆的离心率。
椭圆的性质:
1、顶点:A(a,0),B(-a,0),C(0,b)和D(0,-b)。
2、轴:对称轴:x轴,y轴;长轴长|AB|=2a,短轴长|CD|=2b,a为长半轴长,b为短半轴长。
3、焦点:F1(-c,0),F2(c,0)。
4、焦距: 。
。
5、离心率: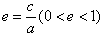 ;
;
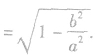
离心率对椭圆形状的影响:e越接近1,c就越接近a,从而b就越小,椭圆就越扁;e越接近0,c就越接近0,从而b就越大,椭圆就越圆;
6、椭圆的范围和对称性: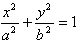 (a>b>0)中-a≤x≤a,-b≤y≤b,对称中心是原点,对称轴是坐标轴。
(a>b>0)中-a≤x≤a,-b≤y≤b,对称中心是原点,对称轴是坐标轴。 。
。
利用椭圆的几何性质解题:
利用椭圆的几何性质可以求离心率 及椭圆的标准方程.要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力。
及椭圆的标准方程.要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力。
椭圆中求最值的方法:
求最值有两种方法:
(1)利用函数最值的探求方法利用函数最值的探求方法,将其转化为函数的最值问题来处理.此时应充分注意椭圆中x,y的范围,常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义,寻找图形中的几何元素、几何量之间的关系.
椭圆中离心率的求法:
在求离心率时关键是从题目条件中找到关于a,b,c的两个方程或从题目中得到的图形中找到a,b,c的关系式,从而求离心率或离心率的取值范围.
圆锥曲线的综合问题:
1、圆锥曲线的范围问题有两种常用方法:
(1)寻找合理的不等式,常见有△>0和弦的中点在曲线内部;
(2)所求量可表示为另一变量的函数,求函数的值域。
2、圆锥曲线的最值、定值及过定点等难点问题。
直线与圆锥曲线的位置关系:
(1)从几何角度来看,直线和圆锥曲线有三种位置关系:相离、相切和相交,相离是直线和圆锥曲线没有公共点,相切是直线和圆锥曲线有唯一公共点,相交是直线与圆锥曲线有两个不同的公共点,并特别注意直线与双曲线、抛物线有唯一公共点时,并不一定是相切,如直线与双曲线的渐近线平行时,与双曲线有唯一公共点,但这时直线与双曲线相交;直线平行(重合)于抛物线的对称轴时,与抛物线有唯一公共点,但这时直线与抛物线相交,故直线与双曲线、抛物线有唯一公共点时可能是相切,也可能是相交,直线与这两种曲线相交,可能有两个交点,也可能有一个交点,从而不要以公共点的个数来判断直线与曲线的位置关系,但由位置关系可以确定公共点的个数.
(2)从代数角度来看,可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系.设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0.
①若a=0,当圆锥曲线是双曲线时,直线l与双曲线的渐近线平行或重合;当圆锥曲线是抛物线时,直线l与抛物线的对称轴平行或重合.
②若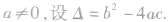
当Δ>0时,直线和圆锥曲线相交于不同两点,相交.
当Δ=0时,直线和圆锥曲线相切于一点,相切.
当Δ<0时,直线和圆锥曲线没有公共点,相离.
直线与圆锥曲线相交的弦长公式:
若直线l与圆锥曲线F(x,y)=0相交于A,B两点,求弦AB的长可用下列两种方法:
(1)求交点法:把直线的方程与圆锥曲线的方程联立,解得点A,B的坐标,然后用两点间距离公式,便得到弦AB的长,一般来说,这种方法较为麻烦.
(2)韦达定理法:
不求交点坐标,可用韦达定理求解.若直线l的方程用y=kx+m或x=n表示.


与“已知椭圆E:x2a2+y2b2=1(a>b>0)的离心率e=22,在椭圆E上...”考查相似的试题有:
- 已知曲线C1:|x|a+|y|b=1(a>b>0)所围成的封闭图形的面积为45,曲线C1的内切圆半径为253.记C2为以曲线C1与坐标轴的交点为顶...
- F1、F2是椭圆x2a2+y29=1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=______.
- 已知椭圆的方程为x2a2+y2b2=1(a>b>0),它的一个焦点与抛物线y2=8x的焦点重合,离心率e=255,过椭圆的右焦点F作与坐标轴不...
- 过轴正半轴上一点,作圆的两条切线,切点分别为,若,则的最小值为( )A.1B.C.2D.3
- 已知双曲线过点(4,),渐近线方程为y=±x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距...
- 看下图回答问题
- 对任意m∈R,曲线x2-y2+mx-my-m-3=0都经过定点( )A.(2,1)B.(1,2)C.(3,2)D.(-2,-3)
- 已知点,直线:,为平面上的动点,过点作直线的垂线,垂足为,且.(1)求动点的轨迹的方程;(2)已知圆过定点,圆心在轨迹...
- 设有抛物线C:y=-x2+92x-4,通过原点O作C的切线y=mx,使切点P在第一象限.(1)求m的值,以及P的坐标;(2)过点P作切线的垂...
- 在平面直角坐标系xOy中,设点、,定义:.已知点,点M为直线上的动点,则使取最小值时点M坐标是.