已知定义在（﹣1，1）上的函数f（x），满足，并且x，y∈（﹣1，1）都有成立，对于数列{xn}，有．（Ⅰ）求f（0），并证明f（x）为奇函,高中一年级,数学试题,函数的奇偶性、周期性考点,等比数列的通项公式考点,反证法与放缩法考点,好技网

解答题
已知定义在（﹣1，1）上的函数f（x），满足，并且x，y∈（﹣1，1）都有成立，对于数列{x_n}，有．
（Ⅰ）求f（0），并证明f（x）为奇函数；
（Ⅱ）求数列{f（x_n）}的通项公式；
（Ⅲ）对于(II）中的数列{f（x_n）}，
证明：（n∈N*）．

本题信息：2011年北京期末题数学解答题难度极难来源:王东（高中数学）
本题答案
查看答案

本试题 “已知定义在（﹣1，1）上的函数f（x），满足，并且x，y∈（﹣1，1）都有成立，对于数列{xn}，有．（Ⅰ）求f（0），并证明f（x）为奇函数；（Ⅱ）求数列{f（xn）}...” 主要考查您对
函数的奇偶性、周期性

等比数列的通项公式

反证法与放缩法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

函数的奇偶性、周期性
等比数列的通项公式
反证法与放缩法

函数的奇偶性定义：

偶函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），则称函数f（x）为偶函数。
奇函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）＝-f（x），那么函数f（x）是奇函数。

函数的周期性：

（1）定义：若T为非零常数，对于定义域内的任一x，使f（x+T）=f（x）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。
周期函数定义域必是无界的。
（2）若T是周期，则k·T（k≠0，k∈Z）也是周期，所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期，如常函数f（x）=C。

奇函数与偶函数性质：

（1）奇函数与偶函数的图像的对称性：奇函数的图像关于原点对称，偶函数的图像关于y轴对称。
（3）在公共定义域内，①两个奇函数的和是奇函数，两个奇函数的积是偶函数； ②两个偶函数的和、积是偶函数； ③一个奇函数，一个偶函数的积是奇函数。

注：定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．

1、函数是奇函数或偶函数的前提定义域必须关于原点对称；定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．

2、函数的周期性令a , b 均不为零，若：
（1）函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
（2）函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
（3）函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
（4）函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|2a|
（5）函数y = f(x) 存在 f(x + a) = 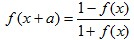==> 函数最小正周期 T=|4a|

等比数列的通项公式:

a_n=a₁q^n-1，q≠0，n∈N^*。

等比数列的通项公式的理解：

①在已知a₁和q的前提下，利用通项公式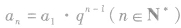可求出等比数列中的任意一项；
②在已知等比数列中任意两项的前提下，使用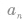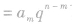可求等比数列中任何一项；
③用函数的观点看等比数列的通项，等比数列{a_n}的通项公式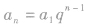，可以改写为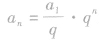．当q>o，且q≠1时，y=q^x是一个指数函数，而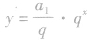是一个不为0的常数与指数函数的积，因此等比数列{a_n}的图象是函数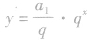的图象上的一群孤立的点；
④通项公式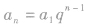亦可用以下方法推导出来：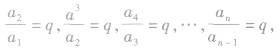

将以上（n一1）个等式相乘，便可得到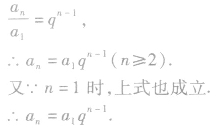

⑤用方程的观点看通项公式．在a_n，q，a₁，n中，知三求一。

反证法的定义：

有些不等式无法利用题设的已知条件直接证明，我们可以用间接的方法——反证法去证明，即通过否定原结论——导出矛盾——从而达到肯定原结论的目的。

放缩法的定义：

把原不等式放大或缩小成一个恰好可以化简的形式，比较常用的方法是把分母或分子适当放大或缩小（减去或加上一个正数）使不等式简化易证。

反证法证题的步骤：

若A成立，求证B成立。
共分三步：
（1）提出与结论相反的假设；如负数的反面是非负数，正数的反面是非正数即0和负数；
（2）从假设出发，经过推理，得出矛盾；（必须由假设出发进行推理否则不是反证法或证错）；
（3）由矛盾判定假设不正确，从而肯定命题的结论正确.矛盾：与定义、公理、定理、公式、性质等一切已有的结论矛盾甚至自相矛盾。
反证法是一种间接证明命题的基本方法。在证明一个数学命题时，如果运用直接证明法比较困难或难以证明时，可运用反证法进行证明。

放缩法的意义：

放缩法理论依据是不等式的传递性：若,a<b,b<c，则a<c.

放缩法的操作：

若求证P<Q，先证P<P₁<P₂<…<P_n,再证恰有P_n<Q.
需注意：（1）只有同方向才可以放缩，反方向不可。
（2）不能放（缩）得太大（小），否则不会有最后的P_n<Q.

发现相似题

与“已知定义在（﹣1，1）上的函数f（x），满足，并且x，y∈（﹣1...”考查相似的试题有：