本试题 “数学门诊部。(对的打“√”,错的打“×”)(1)比的前项一定,比的后项和比值成反比例。[ ](2)比例尺一定,图上距离和实际距离成正比例。[ ](3)当a=3时,a3 ...” 主要考查您对用字母表示数
比的基本性质
正比例的意义,反比例的意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用字母表示数
- 比的基本性质
- 正比例的意义,反比例的意义
用字母表示数:
含有字母的式子不仅可以表示数量关系,也可以表示数量。还可以简明、概括地表达运算定律和计算公式,方便研究和解决实际问题。
①含有字母的式子中,数字和字母、字母和字母相乘时,乘号可以记作“·”,也可以省略不写。
②在省略乘号的时候,应当把数字写在字母的前面。
③当“1”和任何字母相乘时,“1”可以省略不写。
④由于字母可以表示任何数,在一些式中,对字母表示数的要运行说明,如: (a≠0)。
(a≠0)。
⑤因为字母表示的是数,所以在式子中每一个字母都不注明单位名称,计算结果也不注明单位名称,只在答句中写上单位名称。
用字母表示数的意义:
有助于揭示概念的本质特征,能使数量之间的关系更加简明,更具有普遍意义。使思维过程简约化,易于形成概念系统。
含有字母的式子不仅可以表示数量关系,也可以表示数量。还可以简明、概括地表达运算定律和计算公式,方便研究和解决实际问题。
①含有字母的式子中,数字和字母、字母和字母相乘时,乘号可以记作“·”,也可以省略不写。
②在省略乘号的时候,应当把数字写在字母的前面。
③当“1”和任何字母相乘时,“1”可以省略不写。
④由于字母可以表示任何数,在一些式中,对字母表示数的要运行说明,如:
 (a≠0)。
(a≠0)。 ⑤因为字母表示的是数,所以在式子中每一个字母都不注明单位名称,计算结果也不注明单位名称,只在答句中写上单位名称。
用字母表示数的意义:
有助于揭示概念的本质特征,能使数量之间的关系更加简明,更具有普遍意义。使思维过程简约化,易于形成概念系统。
比的基本性质:
1.比的前项和后项同时扩大或缩小相同的倍数(0除外),比值不变。
2.最简比的前项和后项互为质数,且比的前项、后项都为整数。
3.比值通常用比表示,也可以用分数(分数比)或小数表示。
4.比的后项不能为0 。
5.比的前项除以后项等于比值。
1.比的前项和后项同时扩大或缩小相同的倍数(0除外),比值不变。
2.最简比的前项和后项互为质数,且比的前项、后项都为整数。
3.比值通常用比表示,也可以用分数(分数比)或小数表示。
4.比的后项不能为0 。
5.比的前项除以后项等于比值。
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: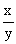 =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。
正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是(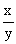 =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。
判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
发现相似题
与“数学门诊部。(对的打“√”,错的打“×”)(1)比的前项一定,比...”考查相似的试题有:
- 小红有a枝铅笔,每枝铅笔0.5元,那么a枝铅笔共花______元.
- 小军有一本连环画,共a页,他每天看h页,看了3天,还剩______页;如果a=100,h=25,那么剩下______页.
- 一筐苹果连筐重36千克,筐重a千克,苹果重______千克.
- 一个比的比值是,如果把它的前项和后项同时扩大3倍,这时的比值( ) A.不变 B.扩大3倍 C.扩大9倍
- 仔细审题,作判断。(对的打√,错的打×,第4题要说明理由。)1.在圆里画出的线段中,直径是最长的一条。[ ]2.2吨铁的和1吨...
- 总价和单价成正比例.______(判断对错)
- 比的后项一定,比的前项与比值成反比例。[ ]
- B1圆锥体积一定,底面积和高成反比例.______.E1
- 关于正方形的周长,边长与面积,下面描述正确的是[ ]A.面积和边长成正比例B.周长与面积成正比例C.周长与边长成正比例
- 下列式子中,X与Y成反比例的是( )A.X+Y=10B.10X=YC.Y=10X