本试题 “如图,在六面体ABCDEFG中,平面ABC∥平面DEFC,AD⊥平面DEFC,AB⊥AC,ED⊥DG,EF∥DC,且AB=AD=DE=DG=2,AC=EF=l,(Ⅰ)求证:BF∥平面ACGD:(Ⅱ)求二面角D-CC-F的余...” 主要考查您对柱体、椎体、台体的表面积与体积
二面角
直线与平面平行的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 柱体、椎体、台体的表面积与体积
- 二面角
- 直线与平面平行的判定与性质
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
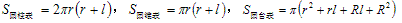
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,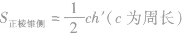 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,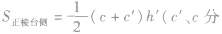  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
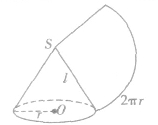 |
圆锥的侧面展开图是扇形: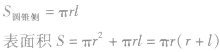 |
 |
| 圆台 |
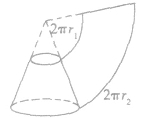 |
圆台的侧面展开图是扇环: |
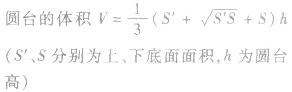 |
| 球 |
 |
 |
 |
半平面的定义:
一条直线把平面分成两个部分,每一部分都叫做半平面.
二面角的定义:
从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
二面角的平面角:
以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角。 一个平面角的大小可用它的平面的大小来衡量,二面角的平面角是多少度,就说这个二面角是多少度。二面角大小的取值范围是[0,180°]。
直二面角:
平面角是直角的二面角叫直二面角。两相交平面如果所组成的二面角是直二面角,那么这两个平面垂直;反过来,如果两个平面垂直,那么所成的二面角为直二面角。
二面角的平面角具有下列性质:
a.二面角的棱垂直于它的平面角所在的平面,即l⊥平面AOB.
b.从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.
c.二面角的平面角所在的平面与二面角的两个面都垂直,即平面AOB⊥α,平面AOB⊥α.
求二面角的方法:
(1)定义法:通过二面角的平面角来求;找出或作出二面角的平面角;证明其符合定义;通过解三角形,计算出二面角的平面角.上述过程可概括为一作(找)、二证、三计算”.
(2)三垂线法:已知二面角其中一个面内一点到另一个面的垂线,用三垂线定理或其逆定理作出平面角.
(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直.
(4)射影法:利用面积射影定理求二面角的大小;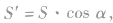 其中S为二面角一个面内平面图形的面积,S′是这个平面图形在另一个面上的射影图形的面积,α为二面角的大小.
其中S为二面角一个面内平面图形的面积,S′是这个平面图形在另一个面上的射影图形的面积,α为二面角的大小.
(5)向量法:设二面角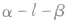 的平面角为θ.
的平面角为θ.
①如果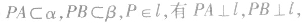 那么
那么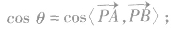
②设向量m、n分别为平面α和平面β的法向量![]() 是相等还是互补,根据具体图形判断。
是相等还是互补,根据具体图形判断。
对二面角定义的理解:
根据这个定义,两个平面相交成4个二面角,其中相对的两个二面角的大小相等,如果这4个二面角中有1个是直二面角,则这4个二面角都是直二面角,这时两个平面互相垂直.按照定义,欲证两个平面互相垂直,或者欲证某个二面角是直二面角,只需证明它的平面角是直角,两个平面相交,如果交成的二面角不是直二面角,那么必有一对锐二面角和一对钝二面角,今后,两个平面所成的角是指其中的一对锐二面角.并注意两个平面所成的角与二面角的区别.
线面平行的定义:
若直线和平面无公共点,则称直线和平面平行。
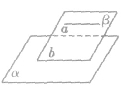
线面平行的判定定理:
平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。 线线平行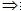 线面平行
线面平行
符号语言:
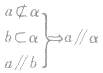
线面平行的性质定理:
如果一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。 线面平行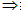 线线平行
线线平行
符号语言:
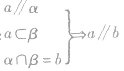
证明直线与平面平行的常用方法:
(l)反证法,即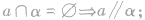
(2)判定定理法,即
(3)面面平行的性质定理,即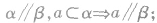
(4)向量法,平面外的直线 的方向向量n与平面
的方向向量n与平面 的法向量n垂直,则直线
的法向量n垂直,则直线 与平面
与平面 平行,即
平行,即
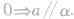
与“如图,在六面体ABCDEFG中,平面ABC∥平面DEFC,AD⊥平面DEFC,A...”考查相似的试题有:
- 一个正四棱柱的各个顶点在一个直径为4cm的球面上.如果正四棱柱的底面边长为2cm,那么该棱柱的表面积为______cm2.
- 已知两个几何体的三视图如下,试求它们的表面积和体积。单位:CM图(2 图(1)
- 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折...
- 棱长都是1的三棱锥的表面积为( )A.3B.23C.33D.43
- 若圆锥的底面直径和高都等于2R,则该圆锥的体积为[ ]A.πR3B.2πR3C.πR3D.4πR3
- 已知正方形ABCD的边长为2,E,F分别为BC,DC的中点,沿AE,EF,AF折成一个四面体,使B,C,D三点重合,则这个四面体的体积为_...
- 如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF=23FD=4.沿直线EF将△AEF翻折成△A′EF,使平面A′EF⊥平面BEF.(Ⅰ)求...
- 在正方体中,M是棱的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )A.B.C.D.
- 在直角坐标系中,,沿轴把直角坐标系折成的二面角,则此时线段的长度为( )A.B.C.D.
- 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=,OA⊥底面ABCD,OA=2, M为OA的中点,N为BC的中点。(1) 证明:直...