本试题 “下列四种说法:(1)命题“∃x∈R,使得x2+1>3x”的否定是“∀x∈R,都有x2+1≤3x”.(2)若a,b∈R,则“log3a>log3b”是“()a<()b”的必要不充分条件(3)把函数y=sin...” 主要考查您对全称量词与存在性量词
对数函数的图象与性质
函数y=Asin(wx+φ)的图象与性质
相等向量与共线向量的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 全称量词与存在性量词
- 对数函数的图象与性质
- 函数y=Asin(wx+φ)的图象与性质
- 相等向量与共线向量的定义
1、全称量词与全称命题:
①全称量词:短语“对所有的”,“对任意的”在陈述中表示整体或全部的含义,逻辑中通常叫做全称量词,并用符号“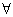 ”表示;
”表示;
②全称命题:含有全称量词的命题,叫做全称命题
③全称命题的格式:“对M中任意一个x,有p(x)成立”的命题,记为?x∈M,p(x),读作“对任意x属于M,有p(x)成立”。
2、存在量词与特称命题:
①存在量词:短语“存在一个”,“至少有一个”在陈述中表示个别或者一部分的含义,在逻辑中通常叫做存在量词,并用符号“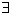 ”表示。
”表示。
②特称命题:含有存在量词的命题,叫做特称命题;
③“存在M中的一个x0,使p(x0)成立”的命题,记为?x0∈M,p(x0),读作“存在一个x0属于M,使p(x0)成立”。
3、全称命题的否定:
一般地,对于含有一个量词的全称命题的否定,有下面的结论:
全称命题p: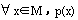 ,它的否命题
,它的否命题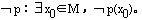
4、特称命题的否定:
一般地,对于含有一个量词的特称命题的否定,有下面的结论:
特称命题p: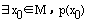 ,其否定命题
,其否定命题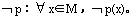
对数函数的图形:
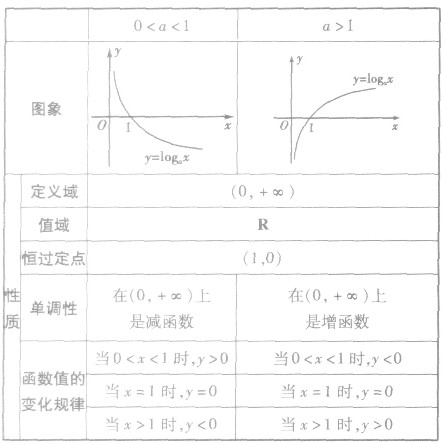
对数函数的图象与性质:
对数函数与指数函数的对比:
(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,它们是减函数.
(3)指数函数与对数函数的联系与区别: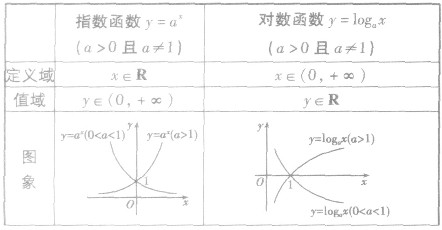
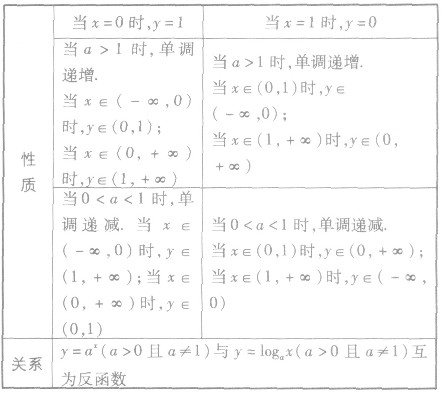
对数函数单调性的讨论:
解决与对数函数有关的函数单调性问题的关键:一是看底数是否大于l,当底数未明确给出时,则应对底数a是否大于1进行讨论;二是运用复合法来判断其单调性,但应注意中间变量的取值范围;三要注意其定义域(这是一个隐形陷阱),也就是要坚持“定义域优先”的原则.
利用对数函数的图象解题:
涉及对数型函数的图象时,一般从最基本的对数函数的图象人手,通过平移、伸缩、对称变换得到对数型函数的图象,特别地,要注意底数a>l与O<a<l的两种不同情况,
底数对函数值大小的影响:
1.在同一坐标系中分别作出函数
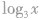 的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
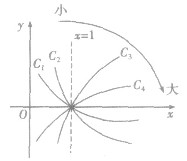
2.类似地,在同一坐标系中分别作出
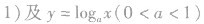 的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如
的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如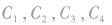 分别对应函数
分别对应函数
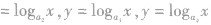 ,则必有
,则必有
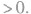
函数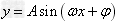 的图象:
的图象:
1、振幅、周期、频率、相位、初相:函数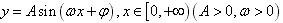 ,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=
,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=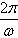 ,称为这个振动的周期,
,称为这个振动的周期,
单位时间内往返振动的次数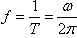 称为振动的频率,
称为振动的频率,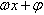 称为相位,x=0时的相位叫初相。
称为相位,x=0时的相位叫初相。
2、用“五点法”作函数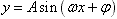 的简图主要通过变量代换,设X=
的简图主要通过变量代换,设X=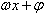 由X取0,
由X取0,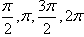 来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
3、函数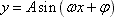 +K的图象与y=sinx的图象的关系:
+K的图象与y=sinx的图象的关系:
把y=sinx的图象纵坐标不变,横坐标向左(φ>0)或向右(φ<0), y=sin(x+φ)
y=sin(x+φ)
把y=sin(x+φ)的图象纵坐标不变,横坐标变为原来的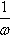 ,
, y=sin(ωx+φ)
y=sin(ωx+φ)
把y=sin(ωx+φ)的图象横坐标不变,纵坐标变为原来的A倍, y=Asin(x+φ)
y=Asin(x+φ)
把y=Asin(x+φ)的图象横坐标不变,纵坐标向上(k>0)或向下(k<0), y=Asin(x+φ)+K;
y=Asin(x+φ)+K;
若由y=sin(ωx)得到y=sin(ωx+φ)的图象,则向左或向右平移 个单位。
个单位。
函数y=Asin(x+φ)的性质:
1、y=Asin(x+φ)的周期为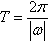 ;
;
2、y=Asin(x+φ)的的对称轴方程是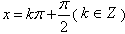 ,对称中心(kπ,0)。
,对称中心(kπ,0)。
相等向量的定义:
长度相等且方向相同的两个向量叫相等向量。
共线向量的定义:
方向相同或相反的非零向量,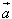 平行于
平行于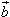 ,记作:
,记作: 。
。
规定零向量和任何向量平行。
注意:相等向量一定是共线向量,但共线向量不一定相等。表示共线向量的有向线段不一定在同一直线上,向量可以平移。
平行向量与相等向量的关系:
(l)平行向量只要求方向相同或相反即可,用有向线段表示平行向量时,向量所在的直线重合或平行.
(2)平行向量要求两个向量均为非零向量,规定:零向量与任一向量平行,记作 ;相等向量则没有这个限制,零向量与零向量相等.
;相等向量则没有这个限制,零向量与零向量相等.
(3)借助相等向量,可以把一组平行向量移动到同一直线上,因此,平行向量也叫做共线向量.(4)平行向量不一定是相等向量,但相等向量一定是平行向量.
向量共线的理解:
(1)两个非零向量平行的充要条件是这两个向量所在直线平行或重合.
(2)两个平行的非零向量在其方向与模两个要素上可能出现以下四种情况:
①方向相同,长度相同;
②方向相同,长度不同;
③方向相反,长度相同;
④方向相反,长度不同,
两个向量相等的理解:
(1)两个向量的长度相等,这两个向量不一定相等.
(2)两个向量相等,它们的起点和终点不一定相同.
(3)若a=b,b=c,则必有a=c.
与“下列四种说法:(1)命题“∃x∈R,使得x2+1>3x”的否定是“∀x∈R...”考查相似的试题有:
- 命题“∀a>b,都有a2>b2”的否定是______.
- 设,则[ ]A.a<b<cB.b<c<aC.c<b<aD.c<a<b
- 设A(x1,y1),B(x2,y2)是函数f(x)=12+log2x1-x的图象上任意两点,且OM=12(OA+OB),已知M的横坐标为12.(1)求证:M点的...
- 设lg2x-lgx2-2=0的两根是α、β,则logαβ+logβα的值是( )A.-4B.-2C.1D.3
- 下列格式正确的是[ ]A.=B.loga(b+c)=logab●logac(a>0,a≠1)C.a2a4a8=a2×4×8D.(ab)n=anbn(n∈N*)
- 已知集合A={2,3,4},B={2,4,6,8},C={(x,y)|x∈A,y∈B,且logxy∈N*},则C中元素个数是( )A.9B.8C.3D.4
- 计算:2log210+log20.04+(-18)-13=______.
- 已知log2m<log2n<0,求m,n的关系.
- 已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<π2)的图象与x轴的交点中,相邻两个交点之间的距离为π2,且图象上...
- 将函数y=sinx的图象先向左平移π3个单位长度,再把横坐标伸长到原来的2倍,纵坐标不变.所得到的曲线对应的函数解析式是______.