本试题 “连掷两次骰子分别得到点数m、n,向量a=(m,n),b=(-1,1)若△ABC中AB 与a同向,CB 与b反向,则∠ABC是钝角的概率是( )A.712B.12C.512D.13” 主要考查您对用数量积表示两个向量的夹角
随机事件及其概率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
- 随机事件及其概率
用数量积表示两个向量的夹角:
设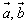 都是非零向量,
都是非零向量,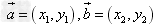 ,θ是
,θ是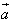 与
与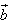 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得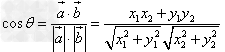 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
随机事件的定义:
在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,随机事件通常用大写英文字母A、B、C等表示。
必然事件的定义:
必然会发生的事件叫做必然事件;
不可能事件:
肯定不会发生的事件叫做不可能事件;
概率的定义:
在大量进行重复试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
m,n的意义:事件A在n次试验中发生了m次。
因0≤m≤n,所以,0≤P(A)≤1,必然事件的概率为1,不可能发生的事件的概率0。
随机事件概率的定义:
对于给定的随机事件A,随着试验次数的增加,事件A发生的频率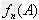 总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
频率的稳定性:
即大量重复试验时,任何结果(事件)出现的频率尽管是随机的,却“稳定”在某一个常数附近,试验的次数越多,频率与这个常数的偏差大的可能性越小,这一常数就成为该事件的概率;
“频率”和“概率”这两个概念的区别是:
频率具有随机性,它反映的是某一随机事件出现的频繁程度,它反映的是随机事件出现的可能性;概率是一个客观常数,它反映了随机事件的属性。
发现相似题
与“连掷两次骰子分别得到点数m、n,向量a=(m,n),b=(-1,1)...”考查相似的试题有:
- 已知△ABC的面积为3,且满足0≤≤6,设和的夹角为θ,则θ的取值范围是( )。
- 已知集合A={-8,-6,-4,-2,0,1,3,5,7},在平面直角坐标系中,点(x,y)的坐标x∈A,y∈A,且x≠y,计算:(1)点(x,y)...
- 已知α,β,γ是平面,a,b是两条不重合的直线,下列说法正确的是( )A.“若a∥b,a⊥α,则b⊥α”是随机事件B.“若a∥b,a⊂α,则b∥α...
- (本小题满分12分)某迷宫有三个通道,进入迷宫的每个人都要经过一个智能门,首次到达此门,系统会随机(即等可能)为你打开一...
- 有10名学生,其中4名男生,6名女生,从中任选2名学生,恰好是2名男生或2名女生的概率是______.
- 将三粒均匀的分别标有:1,2,3,4,5,6的正六面体骰子同时掷出,出现的数字分别为a,b,c,则a,b,c正好是直角三角形三边...
- 一个口袋中装有大小相同的2个红球,3个黑球和4个白球,从口袋中一次摸出一个球,摸出的球不再放回.(1)连续摸球2次,求第一次摸...
- 在投掷一枚硬币的试验中,共投掷了100次,“正面朝上”的频数51,则“正面朝上”的频率为( )A.49B.0.5C.0.51D.0.49
- 同时抛掷两枚骰子,则至少有一个5点或6点的概率是( )A.B.C.D.
- 某校要组建篮球队,需要在各班选拔预备队员,规定投篮成绩一级的可作为入围选手,选拔过程中每人最多投篮5次,且规定在确认已...