本试题 “已知方程x2+y2-2x-4y+m=0。(Ⅰ)若此方程表示圆,求m的取值范围;(Ⅱ)若(Ⅰ)中的圆与直线x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值;(Ⅲ)...” 主要考查您对两直线平行、垂直的判定与性质
圆的标准方程与一般方程
直线与圆的位置关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 两直线平行、垂直的判定与性质
- 圆的标准方程与一般方程
- 直线与圆的位置关系
两直线平行、垂直的判定的文字表述:
平行判断的文字表述:如果两条不重合的直线(存在斜率)平行,则它们的斜率相等;反之,如果两条不重合直线的斜率相等,则它们平行;
垂直判断的文字表述:如果两条直线都有斜率,且它们互相垂直,那么它们斜率之积为-1;反之,如果两条直线的斜率之积为-1,那么它们互相垂直
两直线平行、垂直的判定的符号表示:
1、若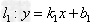 ,
,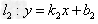
(1)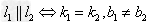 ;
;
(2)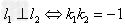 。
。
2、若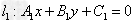 ,
,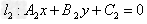 ,且A1、A2、B1、B2都不为零,
,且A1、A2、B1、B2都不为零,
(1)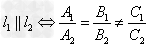 ;
;
(2)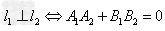 。
。
两直线平行的判断的理解:
 成立的前提条件是两条直线的斜率存在,分别为
成立的前提条件是两条直线的斜率存在,分别为
 当两条直线不重合且斜率均不存在时,
当两条直线不重合且斜率均不存在时,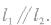
两直线垂直的判断的理解:
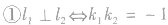 成立的前提条件是斜率都存在且不等于零.
成立的前提条件是斜率都存在且不等于零.
②两条直线中,一条斜率不存在,同时另一条斜率等于零,则两条直线垂直,这样,两条直线垂直的判定就可叙述为:一般地,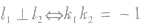 ,或一条直线的斜率不存在,同时另一条直线的斜率等于零。
,或一条直线的斜率不存在,同时另一条直线的斜率等于零。
求与已知直线垂直的直线方程的方法:
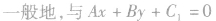 垂直的直线方程可设为
垂直的直线方程可设为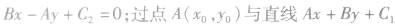
 垂直的直线方程可设为
垂直的直线方程可设为
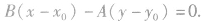
(2)利用互相垂直的直线之间的关系求出斜率,再用点斜式写出直线方程。
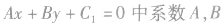 决定直线的斜率,因此,与直线
决定直线的斜率,因此,与直线
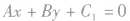 平行的直线方程可设为
平行的直线方程可设为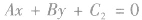 ,这是常常采用的解题技巧。
,这是常常采用的解题技巧。
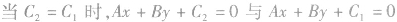 重合。
重合。(2)一般地,经过点

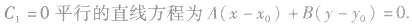
圆的定义:
平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心,定长就是半径。
圆的标准方程:
圆的标准方程 ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为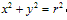 。
。
圆的一般方程:
圆的一般方程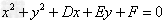
当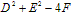 >0时,表示圆心在
>0时,表示圆心在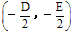 ,半径为
,半径为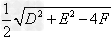 的圆;
的圆;
当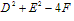 =0时,表示点
=0时,表示点 ;
;
当 <0时,不表示任何图形。
<0时,不表示任何图形。
圆的定义的理解:
(1)定位条件:圆心;定形条件:半径。
(2)当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本的要素是圆心和半径.
圆的方程的理解:
(1)圆的标准方程中含有a,b,r三个独立的系数,因此,确定一个圆需三个独立的条件.其中圆心是圆的定位条件,半径是圆的定形条件.
(2)圆的标准方程的优点在于明确显示了圆心和半径.
(3)圆的一般方程形式的特点:
a.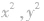 的系数相同且不等于零;
的系数相同且不等于零;
b.不含xy项.
(4)形如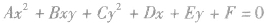 的方程表示圆的条件:
的方程表示圆的条件:
a.A=C≠0;
b.B=0;
c. 即
即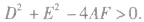
几种特殊位置的圆的方程:
| 条件 | 标准方程 | 一般方程 |
| 圆心在原点 |
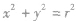 |
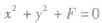 |
| 过原点 |
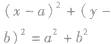 |
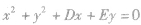 |
| 圆心在x轴上 |
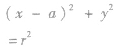 |
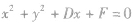 |
| 圆心在y轴上 |
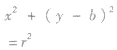 |
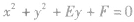 |
| 与x轴相切 |
 |
 |
| 与y轴相切 |
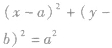 |
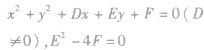 |
|
与x,y轴都相切 |
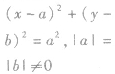 |
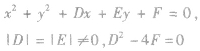 |
| 圆心在x轴上且过原点 |
 |
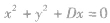 |
| 圆心在y轴上且过原点 |
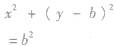 |
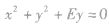 |
直线与圆的位置关系:
由直线与圆的公共点的个数,得出以下直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线。
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做切点。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
其图像如下: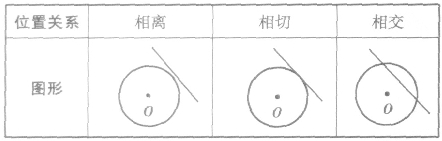
直线和圆的位置关系的性质:
(1)直线l和⊙O相交 d<r
d<r
(2)直线l和⊙O相切 d=r;
d=r;
(3)直线l和⊙O相离 d>r。
d>r。
直线与圆位置关系的判定方法:
(1)代数法:判断直线Ax+By+C=0和圆x2+y2+Dx+Ey+F=0的位置关系,可由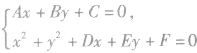
推出mx2+nx+p=0,利用判别式△进行判断.
△>0则直线与圆相交;
△=0则直线与圆相切;
△<0则直线与圆相离.
(2)几何法:已知直线Ax+By+C=0和圆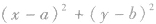
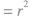 ,圆心到直线的距离
,圆心到直线的距离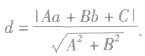
d<r则直线和圆相交;
d=r则直线和圆相切;
d>r则直线和圆相离.
特别提醒:
(1)上述两种方法,以利用圆心到直线的距离进行判定较为简捷,而判别式法也适用于直线与椭圆、双曲线、抛物线位置关系的判断.
(2)直线与圆相交,应抓住半径、弦心距、半弦长组成的直角三角形,可使解法简单.
直线与圆位置关系的判定方法列表如下:
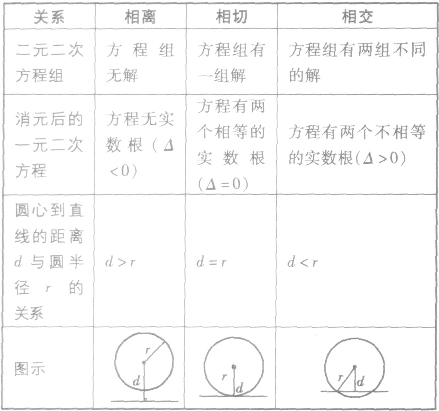
直线与圆相交的弦长公式:
(1)几何法:如图所示,直线l与圆C相交于A、B两点,线段AB的长即为l与圆相交的弦长。
设弦心距为d,半径为r,弦为AB,则有|AB|=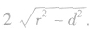
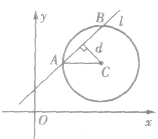
(2)代数法:直线l与圆交于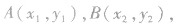 直线l的斜率为k,则有
直线l的斜率为k,则有
当直线AB的倾斜角为直角,即斜率不存在时,|AB|=
与“已知方程x2+y2-2x-4y+m=0。(Ⅰ)若此方程表示圆,求m的取值范...”考查相似的试题有:
- 经过圆(x-1)2+y2=1的圆心M,且与直线x-y=0垂直的直线方程是( )A.x-y+1=0B.x-y-1=0C.x+y-1=0D.x+y+1=0
- 给出下列四个命题:①在△ABC中,∠A>∠B是sinA>sinB的充要条件;②给定命题p,q,若“p或q”为真,则“p且q”为真;③设a,b,m∈R,若a...
- 点P的坐标满足,过点P的直线与圆相交于A、B 两点,则的最小值是( )A. B.4 C. D.3
- 设圆满足:(Ⅰ)截y轴所得弦长为2;(Ⅱ)被x轴分成两段圆弧,其弧长的比为3∶1;在满足条件(Ⅰ)、(Ⅱ)的所有圆中,求圆心到直线l:x-...
- 如图,已知位于y轴左侧的圆C与y轴相切于点(0,1)且被x轴分成的两段圆弧长之比为1:2,过点H(0,t)的直线l于圆C相交于M、N...
- 在平面直角坐标系xOy中,点B与点A(0,2)关于原点O对称,P是动点,AP⊥BP。(Ⅰ)求动点P的轨迹C的方程;(Ⅱ)设直线l:y=x+m...
- 若方程表示的曲线为圆,则的取值范围是( )A.B..C.D.
- 本小题满分10分)求圆心在上,与轴相切,且被直线截得弦长为的圆的方程.
- 设圆C的方程x2+y2-2x-2y-2=0,直线l的方程(m+1)x-my-1=0,对任意实数m,圆C与直线l的位置关系是______.
- 已知离心率为22的椭圆C:x2a2+y2b2=1(a>b>0)过点M(6,1,O是坐标原点.(1)求椭圆C的方程;(2)已知点A、B为椭圆C上相...