本试题 “在平面直角坐标系xOy中，直线l与抛物线y2=4x相交于不同的A、B两点。（1）如果直线l过抛物线的焦点，求的值；（2）如果=-4，证明直线l必过一定点，并求出该定点。” 主要考查您对用坐标表示向量的数量积
直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用坐标表示向量的数量积
- 直线与抛物线的应用
两个向量的数量积的坐标运算:
非零向量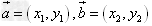
，那么
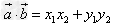，即两个向量的数量积等于它们对应坐标的乘积。
向量的数量积的推广1：
设a=(x,y)，则|a|
=x2+y2 ，或|a|=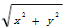
向量的数量积的推广2：
设
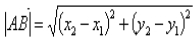
，则
，则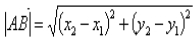 向量的数量积的坐标表示的证明：
已知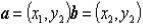
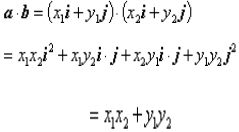
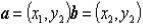，则
，则
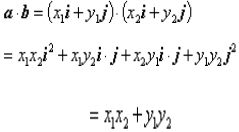
设直线l的方程为：Ax+By+C=0（A、B不同时为零），抛物线的方程为y2=2px（p＞0），将直线的方程代入抛物线的方程，消去y（或x） 得到一元二次方程，进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系，可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定，同时注意过焦点的弦的一些性质，如：
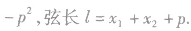
发现相似题
与“在平面直角坐标系xOy中，直线l与抛物线y2=4x相交于不同的A、B...”考查相似的试题有：
- 已知：a=(2cosx，sinx)，b=(cosx，2cosx)，设函数f(x)=a·b-（x∈R），求：（1）f(x)的最小正周期；（2）f(x)的单调递增区间；...
- 设F1、F2分别是椭圆的左、右焦点．（Ⅰ）若P是该椭圆上的一个动点，求PF1·PF2的最大值和最小值；（Ⅱ）设过定点M（0，2）的直线...
- 已知双曲线的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则的最小值为 A．-2B．C．2D．3
- 在平面直角坐标系中，已知点A（1，2），B（3，4），C（5，0）．求：（Ⅰ）|AB|，|AC|；（Ⅱ）AB•AC，COS＜AB，AC＞．
- 在平面直角坐标系中，已知AB=（-1，3），AC=（2，-1），则|BC|=______．
- 设向量满足，则的最大值等于[ ]A.2B.C.D.1
- 在平面直角坐标系xOy中，已知点A（-1，-2），B（2，3），C（-2，-1）。（1）求以线段AB、AC为邻边的平行四边形的两条对角线的...
- 已知向量m=(3sinx4，1)，n=(cosx4，cos2x4)，记f(x)=m•n，（1）求f（x）的值域和单调递增区间；（2）在△ABC中，角A、B、C的对...
- 若点O和点F分别为椭圆的中心和左焦点，点P为椭圆上的任意一点，则的最大值为A.2B.3C.6D.8
- 抛物线y2=2px（p＞0）上有一点Q（4，m）到焦点的距离为5，（1）求p，m的值；（2）过焦点且斜率为1的直线L交抛物线于A，B两点...