本试题 “f(x)是以2为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是______.” 主要考查您对函数的奇偶性、周期性
函数的零点与方程根的联系
二项式定理与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的奇偶性、周期性
- 函数的零点与方程根的联系
- 二项式定理与性质
函数的奇偶性定义:
偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性:
(1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。
奇函数与偶函数性质:
(1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。
注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
2、函数的周期性 令a , b 均不为零,若:
(1)函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
(2)函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
(3)函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
(4)函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|2a|
==> 函数最小正周期 T=|2a|
(5)函数y = f(x) 存在 f(x + a) = 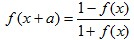 ==> 函数最小正周期 T=|4a|
==> 函数最小正周期 T=|4a|
函数零点的定义:
一般地,如果函数y =f(x)在实数a处的值等于零,即f(a)=o,则a叫做这个函数的零点,有时我们把一个函数的图象与x轴的交点的横坐标,也叫做这个函数的零点。
函数零点具有的性质:
对于任意函数y=(x)只要它的图象是连续不间断的,则有:
(1)当它通过零点时(不是二重零点),函数值变号.如函数f(x)=x2-2x -3的图象在零点-1的左边时,函数值取正号,当它通过第一个零点-1时,函数值由正变为负,在通过第二个零点3时,函数值又由负变为正.
(2)在相邻两个零点之间所有的函数值保持同号,
方程的根与函数的零点的联系:
方程f(x)=0有实根 函数y=f(x)的图像与x轴有交点
函数y=f(x)的图像与x轴有交点 函数y=f(x)有零点
函数y=f(x)有零点
二项式定理:
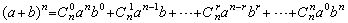 ,
,
它共有n+1项,其中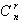 (r=0,1,2…n)叫做二项式系数,
(r=0,1,2…n)叫做二项式系数,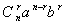 叫做二项式的通项,用Tr+1表示,即通项为展开式的第r+1项.
叫做二项式的通项,用Tr+1表示,即通项为展开式的第r+1项.
二项式系数的性质:
(1)对称性:与首末两端“等距离”的两个二项式系数相等,即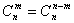 ;
;
(2)增减性与最大值:当r≤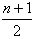 时,二项式系数
时,二项式系数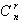 的值逐渐增大;当r≥
的值逐渐增大;当r≥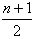 时,
时,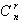 的值逐渐减小,且在中间取得最大值。
的值逐渐减小,且在中间取得最大值。
当n为偶数时,中间一项的二项式系数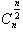 取得最大值;当n为奇数时,中间两项的二项式系数
取得最大值;当n为奇数时,中间两项的二项式系数 相等并同时取最大值。
相等并同时取最大值。
二项式定理的特别提醒:
① 的二项展开式中有(n+1)项,比二项式的次数大1.
的二项展开式中有(n+1)项,比二项式的次数大1.
②二项式系数都是组合数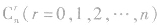 ,它与二项展开式的系数是两个不同的概念,在实际应用中应注意区别“二项式系数”与“二项展开式的系数”。
,它与二项展开式的系数是两个不同的概念,在实际应用中应注意区别“二项式系数”与“二项展开式的系数”。
③二项式定理形式上的特点:
在排列方式上,按照字母a的降幂排列,从第一项起,a的次数由n逐项减小1,直到0,同时字母6按升幂排列,次数由0逐项增加1,直到n,并且形式不能乱.
④二项式定理中的字母a,b是不能交换的,即 与
与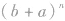 的展开式是有区别的,二者的展开式中的项的排列次序是不同的,注意不要混淆.
的展开式是有区别的,二者的展开式中的项的排列次序是不同的,注意不要混淆.
⑤二项式定理表示一个恒等式,对于任意的实数a,b,该等式都成立,因而,对a,b取不同的特殊值,可以对某些问题的求解提供方便,二项式定理通常有如下两种情形: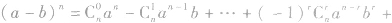
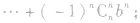
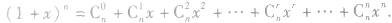
⑥对二项式定理还可以逆用,即
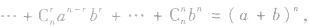 可用于式子的化简。
可用于式子的化简。
二项式定理常见的利用:
方法1:利用二项式证明有关不等式证明有关不等式的方法:
(1)用二项式定理证明组合数不等式时,通常表现为二项式定理的正用或逆用,再结合不等式证明的方法进行论证.
(2)运用时应注意巧妙地构造二项式.证明不等式时,应注意运用放缩法,即对结论不构成影响的若干项可以去掉.
方法2:利用二项式定理证明整除问题或求余数:
(1)利用二项式定理解决整除问题时,关键是要巧妙地构造二项式,其基本做法是:要证明一个式子能被另一个式子整除,只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.
(2)用二项式定理处理整除问题时,通常把底数写成除数(或与除数密切相关的数)与某数的和或差的形式,再用二项式定理展开,只考虑后面(或者是前面)一、二项就可以了.
(3)要注意余数的范围,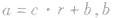 为余数,b∈[0,r),r是除数,利用二项式定理展开变形后,若剩余部分是负数要注意转换.
为余数,b∈[0,r),r是除数,利用二项式定理展开变形后,若剩余部分是负数要注意转换.
方法3:利用二项式进行近似解:
当a的绝对值与1相比很少且n不大时,常用近似公式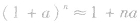 ,因为这时展开式的后面部分
,因为这时展开式的后面部分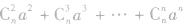 很小,可以忽略不计,类似地,有
很小,可以忽略不计,类似地,有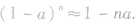 但使用这两个公式时应注意a的条件以及对计算精确度的要求.要根据要求选取展开式中保留的项,以最后一项小数位超要求即可,少了不合要求,多了无用且增加麻烦.
但使用这两个公式时应注意a的条件以及对计算精确度的要求.要根据要求选取展开式中保留的项,以最后一项小数位超要求即可,少了不合要求,多了无用且增加麻烦.
方法4:求展开式特定项:
(1)求展开式中特定项主要是利用通项公式来求,以确定公式中r的取值或范围.
(2)要正确区分二项式系数与展开式系数,对于(a-b)n数展开式中系数最大项问题可以转化为二项式系数的最大问题,要注意系数的正负.
方法5:复制法
利用复制法可以求二项式系数的和及特殊项系数等问题。一般地,对于多项式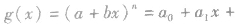


方法6:多项式的展开式问题:
对于多项式(a+b+c)n,我们可以转化为[a+(b+c)]n的形式,再利用二项式定理,求解有关问题。
与“f(x)是以2为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在...”考查相似的试题有:
- 设定义在R上的函数f(x)满足f(x)•f(x+2)=17,若f(1)=2,则f(2007)=( )A.17B.2C.172D.217
- 已知函数f(x)=ex+x-1(x<0)-13x3+2x(x≥0),给出如下四个命题:①f(x)在[2,+∞)上是减函数;②f(x)的最大值是2;③函数y=f...
- 已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若∀x∈[1,2]使得不等式g(2x)-ah...
- 已知函数是定义在上的奇函数,且当时,,则当 时,的解析式为( ).A.B.C.D.
- 已知函数有三个零点,则实数的取值范围为.
- 已知方程(12)x=x13的解x∈(1n+1,1n),则正整数n=______.
- 已知函数f(x)=2x,x∈R.当m取何值时方程|f(x)-2|=m有一个解?两个解?
- 展开式中的常数项为. . . .
- 若的展开式的第8项的系数是,且对于任意实数,有,则的值为__________.
- 展开式中的常数项是_________________.