本试题 “等比数列{cn}满足cn+1+cn=10•4n-1，n∈N*，数列{an}满足cn=2an（1）求{an}的通项公式；（2）数列{bn}满足bn=1an•an+1，Tn为数列{bn}的前n项和．求limn→∞Tn；（...” 主要考查您对等比数列的定义及性质
数列的极限
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等比数列的定义及性质
- 数列的极限
等比数列的定义：
一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做公比，公比通常用字母q表示（q≠0）。
等比数列的性质：
在等比数列｛an｝中，有
（1）若m+n=p+q，m，n，p，q∈N*，则aman=apaq；当m+n=2p时，aman=ap2；
（2）若m，n∈N*，则am=anqm-n；
（3）若公比为q，则｛
｝是以
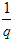为公比的等比数列；
（4）下标成等差数列的项构成等比数列；
（5）
1）若a1＞0，q＞1，则｛an｝为递增数列；
2）a1＜0，q＞1， 则｛an｝为递减数列；
3）a1＞0，0＜q＜1，则｛an｝为递减数列；
4）a1＜0， 0＜q＜1， 则｛an｝为递增数列；
5）q＜0，则｛an｝为摆动数列；若q＝1，则｛an｝为常数列。
如何证明一个数列是等比数列：
证明一个数列是等比数列，只需证明
是一个与n无关的常数即可（或an2=an-1an+1）。
数列的极限定义（描述性的）：
如果当项数n无限增大时，无穷数列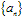
的项an无限地趋近于某个常数a（即
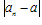无限地接近于0），a叫数列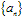的极限，记作
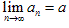，也可记做当n→+∞时，an→a。
数列的极限严格定义：
即ε－N定义：对于任何正数ε（不论它多么小），总存在某正数N，使得当n＞N时，一切an都满足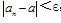
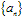，a叫数列的极限。
数列极限的四则运算法则：
若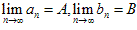
，则
（1）
，
；
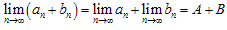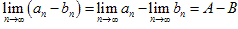（2）
，
；
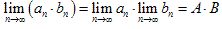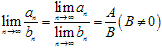（3）
。
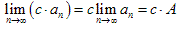前提条件：（1）各数列均有极限，（2）相加减时必须是有限个数列才能用法则。
an无限接近于a的方式有三种：
第一种是递增的数列，an无限接近于a，即an是在常数a的左边无限地趋近于a，如n→+∞时，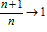
；
第二种是递减数列，an无限地趋近于a，即an是在常数a的右边无限地趋近于a，如n→+∞时，是
；
第三种是摆动数列，an无限地趋近于a，即an是在无限摆动的过程中无限地趋近于a，如n→+∞时，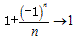
。
一些常用数列的极限：
（1）常数列A，A，A，…的极限是A；
（2）当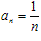
时，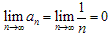
；
（3）当|q|＜1时，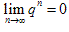
；当q＞1时，
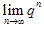不存在；
（4）
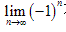不存在，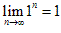
。
（5）无穷等比数列{an}中，首项a1，公比q，前n项和Sn，各项之和S，则
（只有在0＜|q|＜1时）。
与“等比数列{cn}满足cn+1+cn=10•4n-1，n∈N*，数列{an}满足cn=2an...”考查相似的试题有：
- 数列的前项和为，且满足；（1）求与的关系式，并求的通项公式；（2）求和；
- 已知正数数列的前项和为，，数列满足.（Ⅰ）求数列和的通项公式; （Ⅱ）当时，，求数列的前项和．
- 在等比数列中，，则数列的公比为 （ ）A．B．C．D．
- 数列{an}是公比为的等比数列，且1-a2是a1与1+a3的等比中项，前n项和为Sn；数列{bn}是等差数列，b1=8，其前n项和Tn满足Tn=n·bn...
- 用火柴棒摆“金鱼”，如下图所示；按照上面的规律，第个“金鱼”图需要火柴棒的根数为______________。
- （本小题满分10分）设数列前n项和为，且（1）求的通项公式；（2）若数列满足且（n≥1），求数列的通项公式
- 设数列的前n项和，则的值为 ．
- 若等比数列的前n项和为S，a= 6,S= 21,则公比q=
- 数列的前项和为,已知,,则 .
- 定义x1，x2，…，xn的“倒平均数”为nx1+x2+…+xn（n∈N*）．已知数列{an}前n项的“倒平均数”为12n+ 4，记cn=ann+1（n∈N*）．（1）...