本试题 “正整数按下列方法分组:{1},{2,3,4},{5,6,7,8,9},{10,11,12,13, 14,15,16},…,记第n组各数之和为An;由自然数的立方构成下列数组:{03,13}...” 主要考查您对等差数列的前n项和
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差数列的前n项和
等差数列的前n项和的公式:
(1)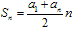 ,(2)
,(2)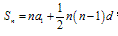 ,(3)
,(3)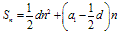 ,(4)
,(4)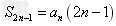
当d≠0时,Sn是关于n的二次函数且常数项为0,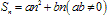
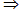 {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
等差数列的前n项和的有关性质:
(1) ,…成等差数列;
,…成等差数列;
(2){an}有2k项时,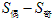 =kd;
=kd;
(3){an}有2k+1项时,S奇=(k+1)ak+1=(k+1)a平, S偶=kak+1=ka平,S奇:S偶=(k+1):k,S奇-S偶=ak+1=a平;
解决等差数列问题常用技巧:
1、等差数列中,已知5个元素:a1,an,n,d, S中的任意3个,便可求出其余2个,即知3求2。
为减少运算量,要注意设元的技巧,如奇数个成等差,可设为…,a-2d,a-d,a,a+d,a+2d,…,偶数个成等差,可设为…,a-3d,a-d,a+d,a+3d,…
2、等差数列{an}中,(1)若ap=q,aq=p,则列方程组可得:d=-1,a1=p+q-1,ap+q=0,S=-(p+q);
(2)当Sp=Sq时(p≠q),数形结合分析可得Sn中最大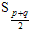 ,Sp+q=0,此时公差d<0。
,Sp+q=0,此时公差d<0。
发现相似题
与“正整数按下列方法分组:{1},{2,3,4},{5,6,7,8,9},{1...”考查相似的试题有:
- 已知数列{an}的前n项和Sn=3n-1,数列{bn}满足b1=1,bn=3bn-1+an(n≥2),记数列{bn}的前n项和为Tn。(Ⅰ)证明{an}为等比数列...
- 已知{an}是一个等差数列,且a2=1,a5=-5,(1)求数列{an}的通项公式;(2)求{an}前n项和Sn的最大值.
- 已知等差数列{an}中,a2+a5+a9+a12=60,那么S13=( )A.390B.195C.180D.120
- 设Sn为等差数列{an}的前n项和,若S3=3,S6=24,则a9=______.
- 设等差数列{an}前n项和为Sn,若a1=-9,a3+a5=-6,则当Sn取最小值时,n等于( )A.5B.6C.7D.8
- 设{an}是公差不为零的等差数列,Sn为其前n项和,满足S6=0,S7=7,求数列{an}的通项公式及前n项和Sn。
- Sn是等差数列{an}的前n项和,且S8=S12,则S20=( )。
- 已知各项均为正数的公比为q的等比数列{an}中,Sn为它的前n项和,a3=19,S2=43,则q=______;设bn=log19an,则数列{bn}的前8项...
- 已知{an}是等差数列,a4+a6=6,其前5项和S5=10,则其公差d=( )。
- 设数列{an}是公差为d的等差数列,其前n项和为Sn.(1)已知a1=1,d=2,(ⅰ)求当n∈N*时,的最小值;(ⅱ)当n∈N*时,求证:;...