返回

高中三年级数学

首页
首页 高中三年级数学知识 空间中直线与直线的位置关系 空间中直线与平面的位置关系 平面与平面的位置关系 试题正文
  • 填空题

    已知m、n是直线，α、β、γ是平面，给出下列命题：
    ①若α⊥β，α∩β=m，n⊥m，则n⊥α或n⊥β；
    ②若α∥β，α∩β=m，β∩γ=n，则m∥n；
    ③若m不垂直于α，则m不可能垂直于α内的无数条直线；
    ④若α∩β=m，n∥m；其中正确的命题的序号是(    )
    （注：把你认为正确的命题的序号都填上）


    本题信息：2012年期末题数学填空题难度一般 来源:褚洪学（高中数学）
  • 本题答案
    查看答案
本试题 “已知m、n是直线，α、β、γ是平面，给出下列命题：①若α⊥β，α∩β=m，n⊥m，则n⊥α或n⊥β；②若α∥β，α∩β=m，β∩γ=n，则m∥n；③若m不垂直于α，则m不可能垂直于α内的无数条...” 主要考查您对

空间中直线与直线的位置关系

空间中直线与平面的位置关系

平面与平面的位置关系

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 空间中直线与直线的位置关系
  • 空间中直线与平面的位置关系
  • 平面与平面的位置关系

异面直线：

不同在任何一个平面内的两条直线。

空间中直线与直线的位置关系有且只有三种 ：

异面直线的判定：

过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线。
用符号语言可表示为：

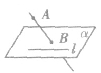
异面直线的画法：
 

 


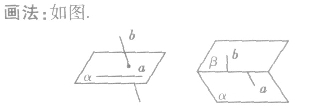
公理4：

平行于同一条直线的两条直线互相平行。

等角定理：

空间中，如果一个角的两边和另一个角的两边分别平行，那么这两角相等或互补。


异面直线的性质：

既不平行，又不相交；


证明线线平行的常用方法：

①利用定义，证两线共面且无公共点；
②利用公理4，证两线同时平行于第三条直线；
③利用线面平行的性质定理把证线线平行转化为证线面平行，转化思想在立体几何中贯穿始终，转化的途径是把空间问题转化为平面问题；
④三角形的中位线；
⑤证两线是平行四边形的对边．


空间中直线与平面的位置关系有且只有三种：

1、直线在平面内——有无数个公共点；
2、直线与平面相交——有且只有一个公共点；
3、直线与平面平行——没有公共点。
直线与平面相交和平行统称为直线在平面外。
直线和平面的位置关系符号表示及相应的图形见下表：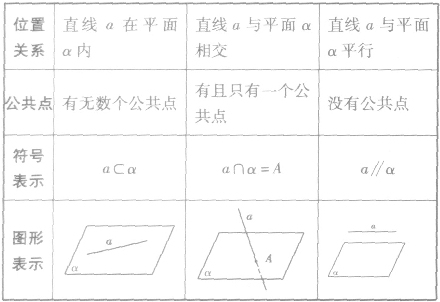


直线和平面的位置关系符号表示及相应的图形见下表：


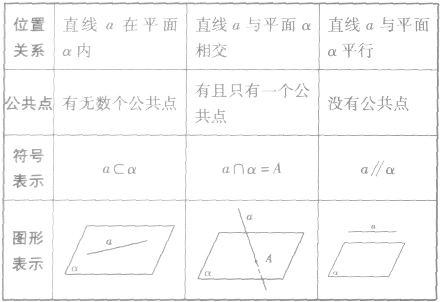
平面与平面的位置关系有且只有两种：

1、两个平面平行——没有公共点；
2、两个平面相交——有一条公共直线。


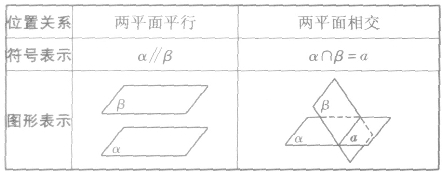
两个平面的位置关系的符号语言及其图形如下表：


发现相似题
与“已知m、n是直线，α、β、γ是平面，给出下列命题：①若α⊥β，α∩β=...”考查相似的试题有：