本试题 “已知函数g(x)=ax3+bx2+cx+d(a≠0)的导函数为f(x),若a+b+c=0,f(0)f(1)>0,设x1,x2是方程f(x)=0的两个根,则|x1﹣x2|的取值范围为[ ]A.B.C.D.” 主要考查您对导数的运算
一元二次方程及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 导数的运算
- 一元二次方程及其应用
常见函数的导数:
(1)C′=0 ;(2)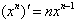 ;(3)
;(3)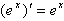 ;(4)
;(4) ;(5)
;(5)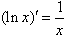 ;(6)
;(6)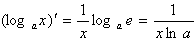 ;(7)
;(7)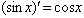 ;(8)
;(8)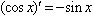
导数的四则运算:
(1)和差: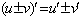
(2)积: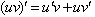
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: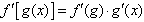
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
一元二次方程的定义:
含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:
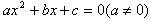 。
。
一元二次方程的应用:
建立一元二次方程模型进行求解,把得到的答案带回实际问题中检验是否合理,来解决实际问题,如打折、营销、增长率问题等。
一元二次方程的根与系数的关系:
如果方程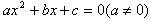 的两个实数根是
的两个实数根是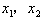 ,那么
,那么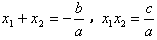 。
。
发现相似题
与“已知函数g(x)=ax3+bx2+cx+d(a≠0)的导函数为f(x),若a+b...”考查相似的试题有:
- 已知f(x)=(2x+1)3-2ax+3a,若f′(-1)=8,则f(-1)=( )A.4B.5C.-2D.-3
- 曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是______.
- 若函数f(x)=sin(3-5x),则f′(x)=______.
- 请先阅读:在等式cos2x=2cos2x-1 (x∈R)的两边对x求导(cos2x)′=(2cos2x-1)′,由求导法则得(-sin2x)·2=4cosx(-sinx),...
- 已知f0(x)=xn,,其中k≤n(n,k∈N+),设F(x)=,x∈[-1,1]。(1)写出f1(1);(2)证明:对任意的x1,x2∈[-1,1],恒有...
- 已知函数f(x)=-cosx+lnx,则f'(1)的值为( )A.sin1-1B.1-sin1C.1+sin1D.-1-sin1
- 设f(x)=(ax+b)sinx+(cx+d)cosx,若已知f′(x)=xcosx,则f(x)=( )A.xsinxB.xsinx-xcosxC.xsinx+cosxD.xcosx
- 对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:f′′(x)是函数y=f(x)的导数f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0)...
- 已知函数y=f(x)ex(x∈R)满足f′(x)>f(x),则f(1)与ef(0)的大小关系为( )A.f(1)=ef(0)B.f(1)<ef(0)C.f(...
- 商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际...