本试题 “已知集合A={a1,a2,…,an}中的元素都是正整数,且a1<a2<…<an,集合A具有性质P:对任意的x,y∈A,且x≠y,有。(1)判断集合{1,2,3,4)是否具有性质P;...” 主要考查您对集合的含义及表示
数列求和的其他方法(倒序相加,错位相减,裂项相加等)
不等式的定义及性质
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合的含义及表示
- 数列求和的其他方法(倒序相加,错位相减,裂项相加等)
- 不等式的定义及性质
- 基本不等式及其应用
集合的概念:
1、集合:一般地我们把一些能够确定的不同对象的全体称为集合(简称集); 集合通常用大写的拉丁字母表示,如A、B、C、……。
元素:集合中每个对象叫做这个集合的元素,元素通常用小写的拉丁字母表示,如a、b、c、……
2、元素与集合的关系:
(1)属于:如果a是集合A的元素,就说a属于A,记作a∈A
(2)不属于:如果a不是集合A的元素,就说a不属于A,记作 3、集合分类根据集合所含元素个属不同,可把集合分为如下几类:
(1)把不含任何元素的集合叫做空集Ф
(2)含有有限个元素的集合叫做有限集
(3)含有无穷个元素的集合叫做无限集
常用数集及其表示方法:
(1)非负整数集(自然数集):全体非负整数的集合.记作N
(2)正整数集:非负整数集内排除0的集.记作N*或N+
(3)整数集:全体整数的集合.记作Z
(4)有理数集:全体有理数的集合.记作Q
(5)实数集:全体实数的集合.记作R
集合中元素的特性:
(1)确定性:给定一个集合,任何对象是不是这个集合的元素是确定的了. 任何一个元素要么属于该集合,要么不属于该集合,二者必具其一。
(2)互异性:集合中的元素一定是不同的.
(3)无序性:集合中的元素没有固定的顺序.
易错点:
(1)自然数集包括数0.
(2)非负整数集内排除0的集.记作N*或N+,Q、Z、R等其它数集内排除0的集,也这样表示,例如,整数集内排除0的集,表示成Z
数列求和的常用方法:
1.裂项相加法:数列中的项形如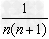 的形式,可以把
的形式,可以把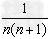 表示为
表示为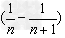 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如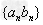 的数列,其中
的数列,其中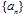 为等差数列,
为等差数列,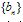 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有:
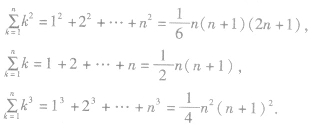
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有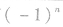 的一类数列,在求
的一类数列,在求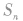 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
不等式的定义:
一般地,用不等号表示不相等关系的式子叫做不等式,常见的不等号有“<”“>”“ ≤”“≥”及“≠”。
严格不等式的定义:
用“>"“<”连接的不等式叫做严格不等式。
非严格不等式的定义:
用“≤”和“≥”连接的不等式叫做非严格不等式.
特别提醒:a=b,a>b中,只要有一个成立,就有a≥b.
不等式的性质:
(1)如果a>b,那么b<a;如果b<a,那么a>b,即a>b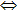 b<a;
b<a;
(2)如果a>b,b>c,那么a>c,即a>b,b>c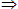 a>c;
a>c;
(3)如果a>b,那么a+c>b+c;
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac<bc;
(5)如果a>b,c>d,那么a+c>b+d;
(6)如果a>b>0,c>d>0,那么ac>bd;
(7)如果a>b>0,那么an>bn(n∈N,n≥2);
(8)如果a>b>0,那么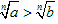 (n∈N,n≥2)。
(n∈N,n≥2)。
不等关系与不等式的区别:
不等关系强调的是量与量之间的关系,可以用符号“<…>…≤”“≥”来表示,也可以用语言表述;
而不等式则是用来表示不等关系的式子,可用“a>b”‘a<b”“a≥b a≤b”等式子来表示,不等关系是通过不等式来体现的.
不等式的分类:
①按成立的条件分:a.绝对不等式:不等式中的字母取任意实数值都恒成立的不等式叫做绝对不等式;b.条件不等式:不等式中的字母取某些允许值才能成立的不等式叫做条件不等式;c.矛盾不等式:不等式中的字母不论取何实数值都不能成立的不等式叫做矛盾不等式;
②按不等号开口方向分:a.同向不等式:不等号方向相同的两个不等式;b.异向不等式:不等号方向相反的两个不等式.
基本不等式:
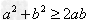 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①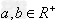 ,
,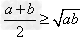 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②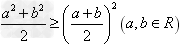 ;③
;③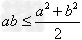 ;④
;④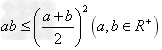 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有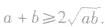
(2)基本不等式又称为均值定理、均值不等式等,其中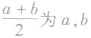 的算术平均数,
的算术平均数,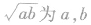 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即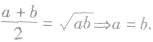
对于两个正数x,y,若已知xy,x+y,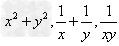 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2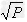 ,
,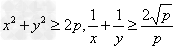 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值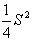 ,
,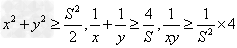 ;
;
(3)已知x2+y2=p,则x+y有最大值为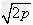 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式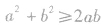 的形式可以是
的形式可以是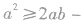
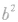 ,也可以是
,也可以是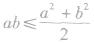 ,还可以是
,还可以是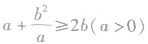 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

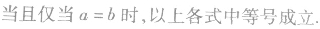
与“已知集合A={a1,a2,…,an}中的元素都是正整数,且a1<a2<…...”考查相似的试题有:
- 已知x、y、z为非零实数,代数式x|x|+y|y|+z|z|+xyz|xyz|的值所组成的集合为M,则下列四种说法中正确的是( )A.0∉MB.2∈MC....
- 已知数列{an}中,a1=a2=1,且an+2-an=1,则数列{an}的前100项和为( )A.2600B.2550C.2651D.2652
- 数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为____________.
- 已知等差数列{an}满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后顺次成为等比数列{bn}的前三项.(Ⅰ)分别...
- 已知二次函数f(x)=x2-ax+a,(a≠0x∈R),有且仅有唯一的实数x值满足f(x)≤0的实数x值满足f(x)≤0.(1)在数列{an}中,满...
- (本小题满分10分)选修4- 5 不等式选讲已知,不等式的解集为M.(I)求M;(II)当时,证明:.
- 已知,且,则的最大值是 .
- 若,则 ( ) A.B.C.D.
- 已知,则xy的最小值是( )。
- 已知,且,则的最大值为