本试题 “若为单位向量,则下面各式中,正确的是( ) A.=1 B. C. D.” 主要考查您对零向量与单位向量
相等向量与共线向量的定义
向量数量积的运算
向量模的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 零向量与单位向量
- 相等向量与共线向量的定义
- 向量数量积的运算
- 向量模的计算
零向量的定义:
长度为0的向量叫零向量,记作: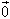 ,注意零向量的方向是任意的。
,注意零向量的方向是任意的。
单位向量的定义:
长度为一个单位长度的向量叫做单位向量,常用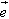 表示。
表示。
零向量和单位向量的理解:
(1)注意零向量与数零的含义与书写的区别,零向量是一个向量所以零向量是有方向的并且规定零向量的方向是任意的;
(2)零向量和单位向量的定义都只是限制了大小;
(3)所有的单位向量都是相等向量是一种错误的说法,因为它们的方向可能不同;所有单位向量的模都相等是一种正确的说法,并且它们的模都等于1.
相等向量的定义:
长度相等且方向相同的两个向量叫相等向量。
共线向量的定义:
方向相同或相反的非零向量,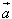 平行于
平行于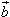 ,记作:
,记作: 。
。
规定零向量和任何向量平行。
注意:相等向量一定是共线向量,但共线向量不一定相等。表示共线向量的有向线段不一定在同一直线上,向量可以平移。
平行向量与相等向量的关系:
(l)平行向量只要求方向相同或相反即可,用有向线段表示平行向量时,向量所在的直线重合或平行.
(2)平行向量要求两个向量均为非零向量,规定:零向量与任一向量平行,记作 ;相等向量则没有这个限制,零向量与零向量相等.
;相等向量则没有这个限制,零向量与零向量相等.
(3)借助相等向量,可以把一组平行向量移动到同一直线上,因此,平行向量也叫做共线向量.(4)平行向量不一定是相等向量,但相等向量一定是平行向量.
向量共线的理解:
(1)两个非零向量平行的充要条件是这两个向量所在直线平行或重合.
(2)两个平行的非零向量在其方向与模两个要素上可能出现以下四种情况:
①方向相同,长度相同;
②方向相同,长度不同;
③方向相反,长度相同;
④方向相反,长度不同,
两个向量相等的理解:
(1)两个向量的长度相等,这两个向量不一定相等.
(2)两个向量相等,它们的起点和终点不一定相同.
(3)若a=b,b=c,则必有a=c.
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量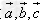 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)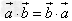 ;
;
(2)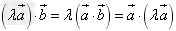 ;
;
(3)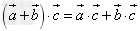 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
向量的模:
设 ,则有向线段
,则有向线段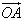 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: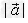 ,则
,则  。
。
向量模的坐标表示:
(1)若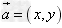 ,则
,则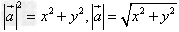 ;
;
(2)若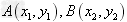 ,那么
,那么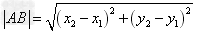 。
。
求向量的模:
求向量的模主要是利用公式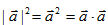 来解。
来解。
与“若为单位向量,则下面各式中,正确的是( ) A.=1 B. C. D.”考查相似的试题有:
- 与向量m=(3,-2)平行的单位向量是______.
- 已知向量a=(sinx,2),b=(cosx,-1).(1)当a∥b时,求sin2x-sin2x的值;(2)求f(x)=(a+b)•a在[-π2,0]上的值域.
- 已知空间向量a,b满足|a|=|b|=1,且a, b的夹角为π3,O为空间直角坐标系的原点,点A、B满足OA=2a+b,OB=3a-b,则△OAB的面积为...
- 已知非零向量a,b的夹角为60°,且|a|=|b|=2,若向量c满足(a-c)•(b-c)=0,则|c|的最大值为______.
- 若向量、的夹角为60°,||=||=1,则·(-)=A、B、C、D、
- 判断下列各命题正确与否:(1)若a≠0,a•b=a•c,则b=c;(2)若a•b=a•c,则b≠c当且仅当a=0时成立;(3)(a•b)c=a(b•c)对...
- 已知向量a=(-cosx,sinx),b=(cosx,3cosx),函数f(x)=a•b.求:(1)函数f(x)的最小正周期(2)函数f(x)在x∈[0,π...
- 若向量a=(cosθ,sinθ),b=(1,-1),则|2a-b|的取值范围是( )A.[2-2,2+2]B.[0,2]C.[0,2]D.[1,3]
- 已知A,B,C三点的坐标分别为A(3,0),B(0,3),C(cosα,sinα),其中α∈(π2,3π2).(1)若|AC|=|BC|,求角α的值;(2)...
- 已知圆(x-2)2+y2=9和直线y=kx交于A,B两点,O是坐标原点,若OA+2OB=O,则|AB|=______.