本试题 “已知椭圆的离心率为,直线:与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切. (1)求椭圆C1的方程; (2)设椭圆C1的左焦点为F1,右焦点F2,直线l1过点F1...” 主要考查您对点关于直线的对称点的坐标
椭圆的标准方程及图象
抛物线的标准方程及图象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 点关于直线的对称点的坐标
- 椭圆的标准方程及图象
- 抛物线的标准方程及图象
对称问题:
(l)点关于点成中心对称的对称中心恰是以这两点为端点的线段的中点,因此中心对称的问题是线段中点坐标公式的应用问题.
设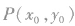 ,对称中心为A(a,b),则P关于A的对称点为
,对称中心为A(a,b),则P关于A的对称点为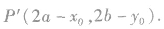
(2)点关于直线成轴对称问题
由轴对称定义知,对称轴即为两对称点连线的“垂直平分线”.利用“垂直”“平分”这两个条件建立方程组,就可求出对称点的坐标.一般情形如下:
设点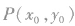 关于直线y=kx+b的对称点为
关于直线y=kx+b的对称点为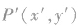 ,则有
,则有 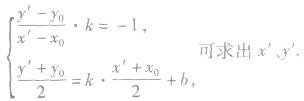
特殊地,点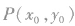 关于直线x=a的对称点为
关于直线x=a的对称点为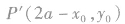 ;点
;点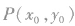 关于直线y=b的对称点为
关于直线y=b的对称点为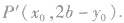
(3)曲线关于点的中心对称、曲线关于直线的轴对称问题,一般是转化为点的中心对称或轴对称(这里既可选特殊点,也可选任意点).一般结论如下:
①曲线f(x,y)=0关于已知点A(a,b)的对称曲线的方程是f(2a-x,2b-y)=0.
②曲线f(x,y)=0关于直线y=kx+b的对称曲线的求法:
设曲线f(x,y)=0上任意一点为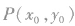 ,P点关于直线y=kx+b的对称点为P′(x,y),则由(2)知,P
,P点关于直线y=kx+b的对称点为P′(x,y),则由(2)知,P

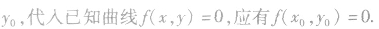 利用坐标代换法就可求出曲线f(x,y)=0关于直线y=kx+b对称的曲线方程。
利用坐标代换法就可求出曲线f(x,y)=0关于直线y=kx+b对称的曲线方程。
几种特殊位置的对称:

(2)曲线f(x,y)=0关于直线x+y+c=0的对称曲线的方程为f(-y-c,-x-c)=0,关于直线x-y+c=0的对称曲线的方程为f(y-c,x+c)=0.
以上这种方法用来解填空题、选择题特别有效,应加以理解与记忆,其规律是当对称轴所在直线方程斜率为1或一1时,将A(x0,y0)中的x0代入对称轴方程x的位置,解出的y是对称点的纵坐标,将A点纵坐标的y0代入对称轴方程y的位置,解出的x是对称点的横坐标.
椭圆的标准方程:
(1)中心在原点,焦点在x轴上: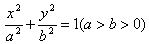 ;
;
(2)中心在原点,焦点在y轴上: 。
。
椭圆的图像:
(1)焦点在x轴: ;
;
(2)焦点在y轴: 。
。
巧记椭圆标准方程的形式:
①椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
②椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上;
③椭圆的标准方程中,三个参数a,b,c满足a2= b2+ c2;
④由椭圆的标准方程可以求出三个参数a,b,c的值.
待定系数法求椭圆的标准方程:
求椭圆的标准方程常用待定系数法,要恰当地选择方程的形式,如果不能确定焦点的位置,那么有两种方法来解决问题:一是分类讨论,全面考虑问题;二是可把椭圆的方程设为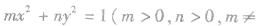 n)用待定系数法求出m,n的值,从而求出标准方程,
n)用待定系数法求出m,n的值,从而求出标准方程,
抛物线的标准方程及图像(见下表):

抛物线的标准方程的理解:
①抛物线的标准方程是指抛物线在标准状态下的方程,即顶点在原点,焦点在坐标轴上;
②抛物线的标准方程中的系数p叫做焦参数,它的几何意义是:焦点到准线的距离.焦点到顶点以及顶点到准线的距离均为
③抛物线的标准方程有四种类型,所以判断其类型是解题的关键,在方程的类型已确定的前提下,由于标准方程只有一个参数p,所以只需一个条件就可以确定一个抛物线的方程;
④对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,得出其异同点。
共同点:
a.原点在抛物线上;
b.焦点都在坐标轴上;
c.准线与焦点所在轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的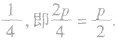
不同点:
a.焦点在x轴上时,方程的右侧为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;
b.开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
求抛物线的标准方程的常用方法:
(1)定义法求抛物线的标准方程:定义法求曲线方程是经常用的一种方法,关键是理解定义的实质及注意条件,将所给条件转化为定义的条件,当然还应注意特殊情况.
(2)待定系数法求抛物线的标准方程:求抛物线标准方程常用的方法是待定系数法,为避免开口不确定,分成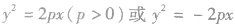 (p>0)两种情况求解的麻烦,可以设成
(p>0)两种情况求解的麻烦,可以设成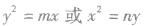 (m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
(m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
与“已知椭圆的离心率为,直线:与以原点为圆心、以椭圆C1的短半轴...”考查相似的试题有:
- 已知抛物线C1:y2=2px(p>0)的焦点F以及椭圆C2:的上、下焦点及左、右顶点均在圆O:x2+y2=1上.(1)求抛物线C1和椭圆C2的...
- 已知椭圆C:(a>b>0)的一个焦点坐标为(1,0),且长轴长是短轴长的倍,(Ⅰ)求椭圆C的方程;(Ⅱ)设O为坐标原点,椭圆C与...
- 已知椭圆中心在坐标原点O,右准线方程为x=1,过左焦点作倾斜角为的直线l与椭圆交于A,B两点。 (1)设点M是线段AB的中点,直...
- 如图,设△OFP的面积为S,已知=1,(1)若,求向量与的夹角θ的取值范围;(2)若S=且≥2,当取最小值时,建立适当的直角坐标系,求...
- 已知椭圆经过点,它的焦距|F1F2|=2,E是椭圆上一点且∠F1EF2=60°,(1)求该椭圆的标准方程;(2)求△F1EF2的面积。
- 已知椭圆C:x2a2+y2b2=1 (a>b>0)的右焦点为F(1,0),左、右顶点分别A、B,其中B点的坐标为(2,0).(Ⅰ)求椭圆C的方程...
- 已知P为圆x2+y2=4上任意一点,Q为点P在x轴上的射影,M为线段PQ的中点,(1)求点M的轨迹C的方程;(2)过点E(0,2)的直线l...
- 在直角坐标系xOy中,中心在原点O,焦点在x轴上的椭圆C上的点(22,1)到两焦点的距离之和为43.(1)求椭圆C 的方程;(2)过...
- 抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
- 抛物线y2=ax 的焦点坐标为(-2,0),则抛物线方程为( ) A.y2=-4x B.y2=4x C.y2=-8x D.y2=8x