本试题 “已知数列{an}的前n项和为Sn,且a2an=S2+Sn对一切正整数n都成立.(1)求a1,a2的值;(2)设a1>0,数列的前n项和为Tn,当n为何值时,Tn最大?并求出Tn的最大值.” 主要考查您对一般数列的项
等差数列的前n项和
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一般数列的项
- 等差数列的前n项和
一般数列的项的定义:
数列中的每一个数叫做这个数列的项。
数列项的性质:
①数列的项具有有序性,一个数列不仅与构成数列的“数”有关,而且与这些数的排列顺序有关,注意与集合中元素的无序性区分开来,;
②数列的项具有可重复性,数列中的数可重复出现,这也要与集合中元素的互异性区分开来:
③注意an与{an}的区别:an表示数列{an}的第n 项,而{an}表示数列a1,a2,…,an,…,
方法提炼:
1.数列最大项、最小项、数列有界性问题可借助数列的单调性来解决,判断单调性时常用(1)作差法;(2)作差法;(3)结合函数图像等方法;
2.若求最大项an,则an满足an≥an+1且an≥an-1;若求最小项an,则an满足an≤an+1且an≤an-1。
等差数列的前n项和的公式:
(1)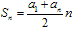 ,(2)
,(2)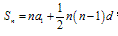 ,(3)
,(3)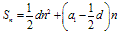 ,(4)
,(4)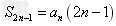
当d≠0时,Sn是关于n的二次函数且常数项为0,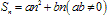
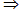 {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
等差数列的前n项和的有关性质:
(1) ,…成等差数列;
,…成等差数列;
(2){an}有2k项时,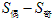 =kd;
=kd;
(3){an}有2k+1项时,S奇=(k+1)ak+1=(k+1)a平, S偶=kak+1=ka平,S奇:S偶=(k+1):k,S奇-S偶=ak+1=a平;
解决等差数列问题常用技巧:
1、等差数列中,已知5个元素:a1,an,n,d, S中的任意3个,便可求出其余2个,即知3求2。
为减少运算量,要注意设元的技巧,如奇数个成等差,可设为…,a-2d,a-d,a,a+d,a+2d,…,偶数个成等差,可设为…,a-3d,a-d,a+d,a+3d,…
2、等差数列{an}中,(1)若ap=q,aq=p,则列方程组可得:d=-1,a1=p+q-1,ap+q=0,S=-(p+q);
(2)当Sp=Sq时(p≠q),数形结合分析可得Sn中最大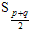 ,Sp+q=0,此时公差d<0。
,Sp+q=0,此时公差d<0。
与“已知数列{an}的前n项和为Sn,且a2an=S2+Sn对一切正整数n都成...”考查相似的试题有:
- 删去正整数数列1,2,3,……中的所有完全平方数,得到一个新数列,这个新数列的第2003项是A.2048B.2049C.2050D.2051
- 已知各项均为正数的数列{an}满足a1=1,且.(Ⅰ)求a2,a3的值;(Ⅱ)求证:是等差数列;(Ⅲ)若,求数列{bn}的前n项和.
- 一辆邮政车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又...
- 甲乙两队进行某决赛,每次比赛一场,采用七局四胜制,即若有一队先胜四场,则此队获胜,比赛就此结束,因两队实力相当,每场...
- 设等差数列{an}的前n项和为Sn且满足S16>0,S17<0,则S1a1,S2a2,…S16a16中最大的项为( )A.S6a6B.S7a7C.S8a8D.S9a9
- 设等差数列{an}的前n项和为Sn,已知a1>0,若S3=S11,则数列{an}的前( )项和最大.
- 如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+...+a7=A.28B.21C.14D.35
- 有两个等差数列{an}、{bn},若a1+a2…+anb1+b2+…bn=2n+1n+3,则a3b3=( )A.76B.118C.139D.89
- 记公差d≠0的等差数列{an}的前n项和为Sn,已知a1=2+2,S3=12+32.(1)求数列{an}的通项公式an及前n项和Sn;(2)记bn=an-2,...
- 已知:等差数列{an}中,a3+a4=15,a2a5=54,公差d<0.(1)求数列{an}的通项公式an;(2)求数列的前n项和Sn的最大值及相应...