本试题 “设复数且则实数等于( )A.B.C.-D.-” 主要考查您对合情推理
演绎推理
复数的概念及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 合情推理
- 演绎推理
- 复数的概念及几何意义
归纳推理的定义:
根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理,叫做归纳推理(简称归纳)。归纳是从特殊到一般的过程,它属于合情推理;
类比推理的定义:
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,叫做类比推理(简称类比)。类比推理是由特殊到特殊的推理。
类比推理的一般步骤:
(1)找出两类事物之间的相似性或一致性;
(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想);
(3)一般地,事物之间的各个性质之间并不是孤立存在的,而是相互制约的。如果两个事物在某些性质上相同或类似,那么它们在另一些性质上也可能相同或类似,类比的结论可能是真的;
(4)在一般情况下,如果类比的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的命题就越可靠。
归纳推理的一般步骤:
①通过观察个别情况发现某些相同性质;
②从已知的相同性质中推出一个明确表达的一般性命题(猜想).
归纳推理和类比推理的特点:
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,统称为合情推理。
归纳推理的应用方法:
归纳推理是由部分到整体、由个别到一般的推理,要注意探求的对象的本质属性与因果关系.与数列有关的问题,要联想等差、等比数列,把握住数的变化规律.
类比推理的应用方法:
合情推理的正确与否来源于平时知识的积累,如平面到空间、长度到面积、面积到体积、平面中的点与空间中的直线、平面中的直线与空间巾的平面.
演绎推理的定义:
从一般性的原理出发,推出某个特殊情况下得结论,我们把这种推理称为演绎推理。演绎推理是由一般到特殊的推理。
演绎推理的一般模式:
“三段论”,
(1)大前提——已知的一般原理;
(2)小前提——所研究的特殊情况;
(3)结论——根据一般原理,对特殊情况做出的判断。
合情推理与演绎推理的区别与联系:
| 合情推理 | 演绎推理 | ||
| 主要区别 | 常用形式 | 归纳、类比 | 三段论 |
| 思维过程的方向 | 归纳推理是从部分到整体,从特殊到一般的推理; 类比推理是从特殊到特殊的推理 |
从一般性的知识的前提推出一个特殊性的知识的结论,即从一般到特殊的推理 | |
| 前提与结论联系的性质 | 结论超过了前提所断定的范围,其结论具有或然性 | 结论不超过前提所断定的范围,前提和结论的联系是必然的 | |
| 应用 | 不能作为数学证明的工具,但它具有创造性思维,对于数学结论的发现十分有用 | 可以作为数学证明的工具,缺少创造性,但它严密的论证有助于科学的理论化和系统化 | |
| 主要联系 |
两者紧密联系,互相依赖,互为补充 | ||
“三段论”可以表示为:
大前提:M是P.
小前提:S是M,
结论:S是P.
利用集合知识说明“三段论”:
若集合M的所有元素都有性质P,S是M的一个子集,那么.S中的所有元素也都具有性质P.
演绎推理的应用方法:
“三段论”是演绎推理的一般模式,其中第一段称为“大前提”,指一个一般原理.第二段称为“小前提”,指一种特殊情况.第三段称为“结论”,指所得结论.当大前提很显然时,常省略不写。
复数的概念:
形如a+bi(a,b∈R)的数叫复数,其中i叫做虚数单位。全体复数所成的集合叫做复数集,用字母C表示。
复数的表示:
复数通常用字母z表示,即z=a+bi(a,b∈R),这一表示形式叫做复数的代数形式,其中a叫复数的实部,b叫复数的虚部。
复数的几何意义:
(1)复平面、实轴、虚轴:
点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做复平面,x轴叫做实轴,y轴叫做虚轴。显然,实轴上的点都表示实数,除原点外,虚轴上的点都表示纯虚数
(2)复数的几何意义:复数集C和复平面内所有的点所成的集合是一一对应关系,即
这是因为,每一个复数有复平面内惟一的一个点和它对应;反过来,复平面内的每一个点,有惟一的一个复数和它对应。
这就是复数的一种几何意义,也就是复数的另一种表示方法,即几何表示方法。
复数的模:
复数z=a+bi(a、b∈R)在复平面上对应的点Z(a,b)到原点的距离叫复数的模,记为|Z|,即|Z|=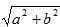
虚数单位i:
(1)它的平方等于-1,即i2=-1;
(2)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立
(3)i与-1的关系:i就是-1的一个平方根,即方程x2=-1的一个根,方程x2=-1的另一个根是-i。
(4)i的周期性:i4n+1=i,i4n+2=-1,i4n+3=-i,i4n=1。
复数模的性质:

复数与实数、虚数、纯虚数及0的关系:
对于复数a+bi(a、b∈R),当且仅当b=0时,复数a+bi(a、b∈R)是实数a;当b≠0时,复数z=a+bi叫做虚数;当a=0且b≠0时,z=bi叫做纯虚数;当且仅当a=b=0时,z就是实数0。
复数集与其它数集之间的关系:
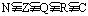 。
。
与“设复数且则实数等于( )A.B.C.-D.-”考查相似的试题有:
- 定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)...
- 有一道解三角形的问题,缺少一个条件.具体如下:“在△ABC中,已知a=3,B=45°,______,求A角的大小.”经推断缺少的条件为三角...
- 已知,则 .
- 定义[x]为不超过x的最大整数,则[-2.1]=
- 在平面内,如果用一条直线去截正方形的一个角,那么截下的一个直角三角形按图所标边长,由勾股定理有。设想正方形换成正方体...
- 若复数,,则复数在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限
- 设i是虚数单位,复数的虚部为________.
- 复数z=(a2+1)-(b2+1)i(a,b∈R)对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限
- 复数的共轭复数是 ( )A.B.C.D.
- 定义运算(,)※(c,d)=-bd,则符合条件(z,1+2)※(1+,1-)=0的复数z的所对应的点在( )A.第一象限B.第二象限C.第三象限D...