本试题 “某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售这种产品的总开支(不含进货费用)总计120万元,在销售过程中发现,年...” 主要考查您对一次函数的性质与应用
二次函数的性质及应用
一元二次不等式及其解法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一次函数的性质与应用
- 二次函数的性质及应用
- 一元二次不等式及其解法
一次函数的定义和图像:
(1)定义:一般地,形如y=kx+b(k、b为常数,k≠0)的函数,叫做一次函数,其中正比例函数是一次函数的特殊情况。
(2)图象:一次函数的图像是一条直线,过(0,b),(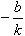 ,0)两点,其中k叫做该直线的斜率,b叫做该直线在y轴上的截距。
,0)两点,其中k叫做该直线的斜率,b叫做该直线在y轴上的截距。
一次函数的性质:
(1)当k>0时,y随x的增大而增大;
(2)当k<0时,y随x的增大而减小。
(3)当b=0时,一次函数变为正比例函数,是奇函数;当b≠0时,它既不是奇函数也不是偶函数。
(4)k的大小表示直线与x轴的倾斜程度
一次函数y=kx+b(k不等于零)的图像:
当k>0时,
若b=0,则图像过第一、三象限;
若b>0,则图像过第一、二、三象限;
若b<0,则图像过第一、三、四象限。
当k>0时,
若b=0,则图像过第二、四象限;
若b>0,则图像过第一、二、四象限;
若b<0,则图像过第二、三、四象限。
应用:应用一次函数解应用题,一般是先写出函数解析式,在依照题意,设法求解。
二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于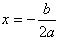 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴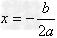 ;
;
③有顶点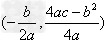 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
①当a>0时,函数f(x)的图象开口向上,在(-∞,-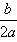 )上是减函数,在[-
)上是减函数,在[- ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-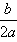 )上是增函数,在[-
)上是增函数,在[-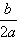 ,+∞)是减函数。
,+∞)是减函数。
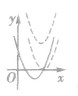
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
 |
值域 | a>0 | a<0 |
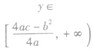 |
 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
| a<0 | 单调性 | a>0 | a<0 |
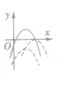 |
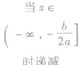 |
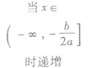 | |
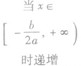 |
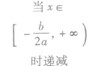 | ||
| 图像特点 |
 | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为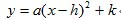 ;
;
(3)双根式:若相应一元二次方程的两个根为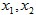 ,则其解析式为
,则其解析式为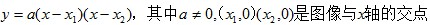 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
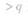 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令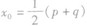 .
.
①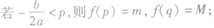
②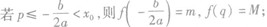
③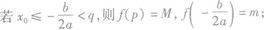
④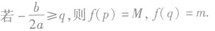
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数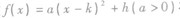 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
一元二次不等式的概念:
只含有一个未知数,并且未知数的最高次数是2 的不等式称为一元二次不等式.
一元二次不等式的解集:
使某个一元二次不等式成立的x的值叫做这个一元二次不等式的解,一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集。
同解不等式:
如果两个不等式的解集相同,那么这两个不等式叫做同解不等式,如果一个不等式变形为另一个不等式时,这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形。
二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:
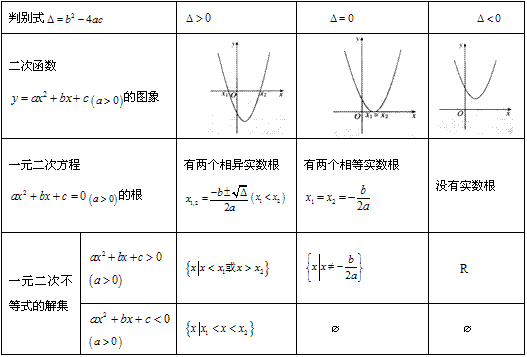
解不等式的过程:
解不等式的过程就是将不等式进行同解变形,化为最简形式的同解不等式的过程.变形时要注意条件的限制,比如:分母是否有意义,定义域是否有限制等.
解一元二次不等式的一般步骤为:
(1)对不等式变形,使一端为零且二次项系数大于零;(2)计算相应的判别式;(3)当△≥0时,求出相应的一元二次方程的根;(4)根据二次函数图象写出一元二次不等式的解集.
解含有参数的一元二次不等式:
(1)要以二次项系数与零的大小作为分类标准进行分类讨论;(2)转化为标准形式的一元二次不等式(即二次项系数大于零)后,再以判别式与零的大小作为分类标准进行分类讨论;(3)如果判别式大于零,但两根的大小还不能确定,此时再以两根的大小作为分类标准进行分类讨论。
与“某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每...”考查相似的试题有:
- 已知函数f(x)=ax2+(b-8)x-a-ab,当x∈(-3,2)时,f(x)>0,当x∈(-∞,-3)∪(2,+∞)时,f(x)<0.(1)求f(x)的...
- 如图,直线y=x与抛物线y=x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点,(1)求点Q的坐标;(2)当P为抛物线上位于线...
- 设a>0,a≠1,函数f(x)=ax2+x+1有最大值,则不等式loga(x-1)>0的解集为________.
- 已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2,x1+x2=1-a,则[ ]A.f(x1)>f(x2)B.f(x1)<f(x2)C.f(x1)=f(x2)D....
- 已知上恒成立,则实数a的取值范围是( )A.B.C.D.
- 若函数y=x2+(2a-1)x+1在区间(-∞,2]上是减函数,则实数a的取值范围是______.
- 函数f(x)=ax2+2(a-1)x+2在区间(-∞,4)上为减函数,则a的取值范围为[ ]A.0<a≤B.0≤a≤C.0<a<D.a>
- 已知函数f(x)=x2-2ax+a的定义域为(1,+∞),且存在最小值-2;(1)求实数a的值;(2)令g(x)=f(x)x,求函数y=g(x)的最值.
- .解关于的不等式:
- 已知不等式ax2-3x+6>4的解集为{x|xb},(1)求a,b;(2)解不等式ax2-(ac+b)x+bc