已知函数f（x）=|x+a|．（Ⅰ）当a=-1时，求不等式f（x）≥|x+1|+1的解集；（Ⅱ）若不等式f（x）+f（-x）＜2存在实数解，,高中,数学试题,函数的零点与方程根的联系考点,绝对值不等式考点,好技网

解答题
已知函数f（x）=|x+a|．
（Ⅰ）当a=-1时，求不等式f（x）≥|x+1|+1的解集；
（Ⅱ）若不等式f（x）+f（-x）＜2存在实数解，求实数a的取值范围．

本题信息：数学解答题难度较难来源:未知
本题答案
查看答案

本试题 “已知函数f（x）=|x+a|．（Ⅰ）当a=-1时，求不等式f（x）≥|x+1|+1的解集；（Ⅱ）若不等式f（x）+f（-x）＜2存在实数解，求实数a的取值范围．” 主要考查您对
函数的零点与方程根的联系

绝对值不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

函数的零点与方程根的联系
绝对值不等式

函数零点的定义：

一般地，如果函数y =f(x)在实数a处的值等于零，即f(a)=o，则a叫做这个函数的零点，有时我们把一个函数的图象与x轴的交点的横坐标，也叫做这个函数的零点。

函数零点具有的性质：

对于任意函数y=(x)只要它的图象是连续不间断的，则有：
(1)当它通过零点时（不是二重零点），函数值变号．如函数f(x)=x²-2x -3的图象在零点-1的左边时，函数值取正号，当它通过第一个零点-1时，函数值由正变为负，在通过第二个零点3时，函数值又由负变为正．
(2)在相邻两个零点之间所有的函数值保持同号，

方程的根与函数的零点的联系：

方程f（x）=0有实根函数y=f（x）的图像与x轴有交点函数y=f（x）有零点

绝对值不等式：

当a>0时，有；
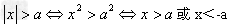或x＜-a 。

绝对值不等式的解法：

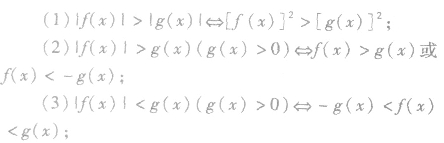
(4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解，也可以用图象法求解。

发现相似题

与“已知函数f（x）=|x+a|．（Ⅰ）当a=-1时，求不等式f（x）≥|x+1|...”考查相似的试题有：