本试题 “设{an}是由正数组成的等比数列,Sn是其前n项和.(1)证明lgSn+lgSn+22<lgSn+1;(2)是否存在常数c>0,使得lg(Sn-c)+lg(Sn+2-c)2=lg(Sn+1-c)成立?并证明...” 主要考查您对对数函数的图象与性质
等比数列的前n项和
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数函数的图象与性质
- 等比数列的前n项和
对数函数的图形:
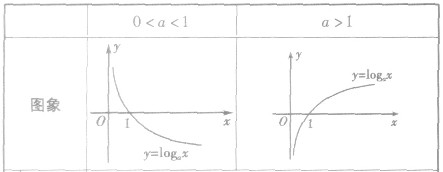
对数函数的图象与性质:
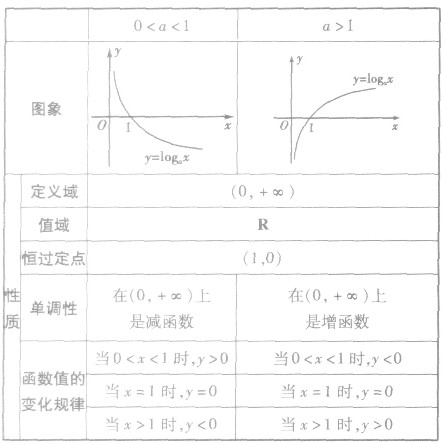
对数函数与指数函数的对比:
(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,它们是减函数.
(3)指数函数与对数函数的联系与区别: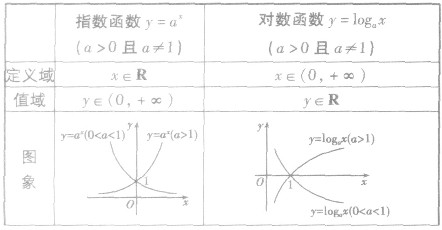
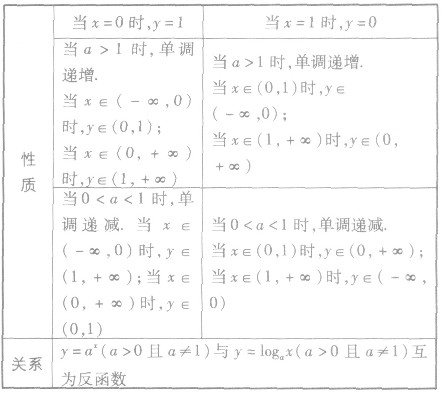
对数函数单调性的讨论:
解决与对数函数有关的函数单调性问题的关键:一是看底数是否大于l,当底数未明确给出时,则应对底数a是否大于1进行讨论;二是运用复合法来判断其单调性,但应注意中间变量的取值范围;三要注意其定义域(这是一个隐形陷阱),也就是要坚持“定义域优先”的原则.
利用对数函数的图象解题:
涉及对数型函数的图象时,一般从最基本的对数函数的图象人手,通过平移、伸缩、对称变换得到对数型函数的图象,特别地,要注意底数a>l与O<a<l的两种不同情况,
底数对函数值大小的影响:
1.在同一坐标系中分别作出函数
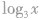 的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
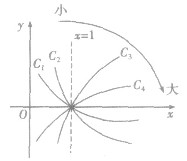
2.类似地,在同一坐标系中分别作出
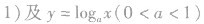 的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如
的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如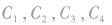 分别对应函数
分别对应函数
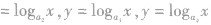 ,则必有
,则必有
等比数列的前n项和公式:
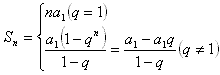 ;
;
等比数列中设元技巧:
已知a1,q,n,an ,Sn中的三个量,求其它两个量,是归结为解方程组问题,知三求二。
注意设元的技巧,如奇数个成等比数列,可设为:…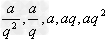 ,…(公比为q),但偶数个数成等比数列时,不能设为…
,…(公比为q),但偶数个数成等比数列时,不能设为…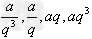 ,…因公比不一定为一个正数,公比为正时可如此设。
,…因公比不一定为一个正数,公比为正时可如此设。
等比数列前n项和公式的变形:
q≠1时,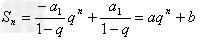 (a≠0,b≠0,a+b=0);
(a≠0,b≠0,a+b=0);
等比数列前n项和常见结论:
一个等比数列有3n项,若前n项之和为S1,中间n项之和为S2,最后n项之和为S3,当q≠-1时,S1,S2,S3为等比数列。
与“设{an}是由正数组成的等比数列,Sn是其前n项和.(1)证明lgS...”考查相似的试题有:
- 定义在[1,64]上的函数f(x)=log2x-1,函数g(x)=-f2(x)+f(x3)(1)求函数g(x)的定义域;(2)求函数g(x)的最值以...
- 计算:log43•log92=______.
- 已知函数f(x)=loga(1+x)-loga(1-x)(a>0且a≠1)(1)讨论f(x)的奇偶性与单调性;(2)若不等式|f(x)|<2的解集为{...
- 已知实数a,b满足0<b<a<1,则下列关系式中可能成立的有①2a=3b;②log2a=log3b;③a2=b3[ ]A.0个B.1个C.2个D.3个
- logab2logb2a=______.
- 已知函数y=log3(mx+1)在(-∞,1)上是减函数,则实数 m的取值范围是______.
- 已知数列{an}满足log3an+1=log3an+1(n∈N*),且a2+a4+a6=9,则的值是A.B.-5C.5D.
- 不等式log(2x-1)(x2-x-5)>0的解集为______.
- 求下列各式中的x的值:(1)ln(x-1)<1 (2)(13)1-x -2<0(3)a2x-1>(1a)x-2,其中a>0且a≠1.
- 函数y=loga(3x﹣2)(a>0,a≠1)的图象过定点[ ]A.(0,)B.(1,0)C.(0,1)D.(,0)