有下面四个判断：①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”是一个假命题②若“p或q”为真命题，则p、q均为真命题③命题“a、b,高中三年级,数学试题,真命题、假命题考点,全称量词与存在性量词考点,好技网

单选题
有下面四个判断：
①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”是一个假命题
②若“p或q”为真命题，则p、q均为真命题
③命题“a、b∈R，a²+b²≥2（a﹣b﹣1）”的否定是：“a、b∈R，a²+b²≤2（a﹣b﹣1）”
④若函数的图象关于原点对称，则a=3
其中正确的个数共有
[ ]

A．0个
B．1个
C．2个
D．3个

本题信息：2012年江西省模拟题数学单选题难度一般来源:朱潇（高中数学）
本题答案
查看答案

本试题 “有下面四个判断：①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”是一个假命题②若“p或q”为真命题，则p、q均为真命题③命题“a、b∈R，a2+b2≥2（a﹣b﹣1）”的否定是：“a...” 主要考查您对
真命题、假命题

全称量词与存在性量词
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

真命题、假命题
全称量词与存在性量词

命题的概念：

1、命题：把语言、符号或式子表达的，可以判断真假的陈述句称为命题；
2、真命题、假命题：判断为真的语句称为真命题，判断为假的语句称为假命题。

注意：

1、并不是所有的语句都是命题，只有能够判断真假的语句才是命题。

2、如果一个语句是命题，则它是真命题或是假命题，二者必具其一。

1、全称量词与全称命题：
①全称量词：短语“对所有的”，“对任意的”在陈述中表示整体或全部的含义，逻辑中通常叫做全称量词，并用符号“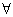”表示；
②全称命题：含有全称量词的命题，叫做全称命题
③全称命题的格式：“对M中任意一个x，有p（x）成立”的命题，记为?x∈M，p（x），读作“对任意x属于M，有p（x）成立”。
2、存在量词与特称命题：
①存在量词：短语“存在一个”，“至少有一个”在陈述中表示个别或者一部分的含义，在逻辑中通常叫做存在量词，并用符号“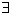”表示。
②特称命题：含有存在量词的命题，叫做特称命题；
③“存在M中的一个x₀，使p（x₀）成立”的命题，记为?x₀∈M，p（x₀），读作“存在一个x₀属于M，使p（x₀）成立”。
3、全称命题的否定：
一般地，对于含有一个量词的全称命题的否定，有下面的结论：
全称命题p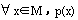：，它的否命题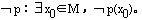
4、特称命题的否定：
一般地，对于含有一个量词的特称命题的否定，有下面的结论：
特称命题p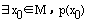：，其否定命题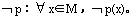

发现相似题

与“有下面四个判断：①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”是...”考查相似的试题有：