本试题 “在等比数列{an}中,若公比q=4,且前三项之和等于21,则该数列的通项公式an=( )。” 主要考查您对等比数列的通项公式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等比数列的通项公式
等比数列的通项公式:
an=a1qn-1,q≠0,n∈N*。
等比数列的通项公式的理解:
①在已知a1和q的前提下,利用通项公式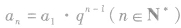 可求出等比数列中的任意一项;
可求出等比数列中的任意一项;
②在已知等比数列中任意两项的前提下,使用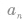
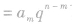 可求等比数列中任何一项;
可求等比数列中任何一项;
③用函数的观点看等比数列的通项,等比数列{an}的通项公式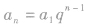 ,可以改写为
,可以改写为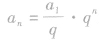 .当q>o,且q≠1时,y=qx是一个指数函数,而
.当q>o,且q≠1时,y=qx是一个指数函数,而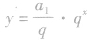 是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数
是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数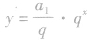 的图象上的一群孤立的点;
的图象上的一群孤立的点;
④通项公式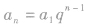 亦可用以下方法推导出来:
亦可用以下方法推导出来: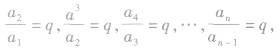
将以上(n一1)个等式相乘,便可得到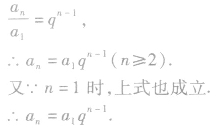
⑤用方程的观点看通项公式.在an,q,a1,n中,知三求一。
发现相似题
与“在等比数列{an}中,若公比q=4,且前三项之和等于21,则该数列...”考查相似的试题有:
- 已知递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4的等差中项,若bn=log2an+1,则数列{bn}的前n项和Sn=______.
- 设Sn是等比数列{an}的前n项和,且S3=74,S6=634.(1)求{an}的通项公式an;(2)设bn=log2an,求数列{bn}的前n项和Tn.
- 某厂产值第二年比第一年增长p%,第三年比第二年增长q%,又这两年的平均增长率为S%,则S与的大小关系是( ) A.S> B.S= C....
- 已知{an}为等比数列,Sn是它的前n项和.若a2•a3=2a1,且a4与a7的等差中项为54,则公比q=______.
- 如图,顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1...
- 如表格中,如果每格填上一个数后,每一横行成等差数列,每一纵列成等比数列,那么x+y+z的值为______2412xYZ
- 已知数列{an}的前n项和满足log2(Sn+1)=n+1,n∈N*,则an=______.
- 已知点(1,12)是函数f(x)=ax(a>0,且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为...
- 在公差为d(d≠0)的等差数列{an}和公比为q的等比数列{bn}中,a2=b1=3,a5=b2,a14=b3,(1)求数列{an}与{bn}的通项公式;(2...
- 已知公差不为0的等差数列{an}的前n项和为Sn,S7=70,且a1,a2,a6成等比数列.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设bn=2Sn+48n...