已知函数f（x）满足f(x)=x3+f ′(23)x2-x+C（其中f ′(23)为f（x）在点x=23处的导数，C为常数）．（1）求函数f,高中,数学试题,函数的单调性与导数的关系考点,定积分的概念及几何意义考点,好技网

解答题
已知函数f（x）满足f(x)=x3+f ′(
2
3
)x2-x+C（其中f ′(
2
3
)为f（x）在点x=
2
3
处的导数，C为常数）．
（1）求函数f（x）的单调区间；
（2）若方程f（x）=0有且只有两个不等的实数根，求常数C；
（3）在（2）的条件下，若f(-
1
3
)＞0，求函数f（x）的图象与x轴围成的封闭图形的面积．

本题信息：数学解答题难度较难来源:未知
本题答案
查看答案

本试题 “已知函数f（x）满足f(x)=x3+f ′(23)x2-x+C（其中f ′(23)为f（x）在点x=23处的导数，C为常数）．（1）求函数f（x）的单调区间；（2）若方程f（x）=0有且只有两...” 主要考查您对
函数的单调性与导数的关系

定积分的概念及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

函数的单调性与导数的关系
定积分的概念及几何意义

导数和函数的单调性的关系：

（1）若f′（x）>0在（a，b）上恒成立，则f（x）在（a，b）上是增函数，f′（x）>0的解集与定义域的交集的对应区间为增区间；
（2）若f′（x）<0在（a，b）上恒成立，则f（x）在（a，b）上是减函数，f′（x）<0的解集与定义域的交集的对应区间为减区间。

利用导数求解多项式函数单调性的一般步骤：

①确定f（x）的定义域；
②计算导数f′（x）；
③求出f′（x）=0的根；
④用f′（x）=0的根将f（x）的定义域分成若干个区间，列表考察这若干个区间内f′（x）的符号，进而确定f（x）的单调区间：f′（x）>0，则f（x）在对应区间上是增函数，对应区间为增区间；f′（x）<0，则f（x）在对应区间上是减函数，对应区间为减区间。

函数的导数和函数的单调性关系特别提醒：

若在某区间上有有限个点使f′(x)=0，在其余的点恒有f′（x）>0，则f(x)仍为增函数（减函数的情形完全类似）．即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件，而不是必要条件。

定积分的定义：

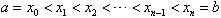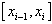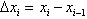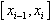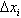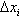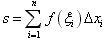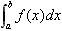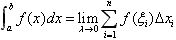设函数f（x）在[a，b]上有界（通常指有最大值和最小值），在a与b之间任意插入n-1个分点，，将区间[a，b]分成n个小区间（i=1，2，…，n），记每个小区间的长度为（i=1，2，…，n），在上任取一点ξ_i，作函数值f（ξ_i）与小区间长度的乘积f（ξ_i）（i=1，2，…，n），并求和，记λ=max{△x_i；i=1，2，…，n }，如果当λ→0时，和s总是趋向于一个定值，则该定值便称为函数f(x)在[a，b]上的定积分，记为，即，其中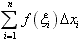，称为函数f(x)在区间[a，b]的积分和。

定积分的几何意义：

定积分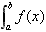在几何上，
当f（x）≥0时，表示由曲线y=f（x）、直线x=a、直线x=b与x轴所围成的曲边梯形的面积；
当f（x）≤0时，表示由曲线y=f（x）、直线x=a、直线x=b与x轴所围成的曲边梯形的面积的负值；
一般情况下，表示介于曲线y=f（x）、两条直线x=a、x=b与x轴之间的个部分面积的代数和。

定积分的性质：

（1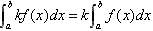）（k为常数）；
（2）；
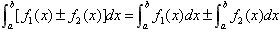（3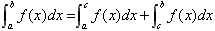）（其中a＜c＜b）。

定积分特别提醒：

①定积分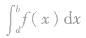不是一个表达式，而是一个常数，它只与被积函数及积分区间有关，而与积分变量的记法无关，例如：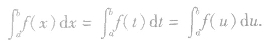
②定义中区间的分法和ξ的取法是任意的，

发现相似题

与“已知函数f（x）满足f(x)=x3+f ′(23)x2-x+C（其中f ′(23)为f（...”考查相似的试题有：