返回

高中数学

首页
首页 高中数学知识 真命题、假命题 基本不等式及其应用 试题正文
  • 单选题
    下列说法正确的是（　　）
    A．a，b∈R，且a＞b，则a2＞b2
    B．若a＞b，c＞d，则 
    a
    c
    ＞
    b
    d
    C．a，b∈R，且ab≠0，则 
    a
    b
    +
    b
    a
    ≥2
    D．a，b∈R，且a＞|b|，则an＞bn（n∈N*）

    本题信息：数学单选题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “下列说法正确的是（ ）A．a，b∈R，且a＞b，则a2＞b2B．若a＞b，c＞d，则 ac＞bdC．a，b∈R，且ab≠0，则 ab+ba≥2D．a，b∈R，且a＞|b|，则an＞bn（n∈N*）” 主要考查您对

真命题、假命题

基本不等式及其应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 真命题、假命题
  • 基本不等式及其应用

命题的概念：

1、命题：把语言、符号或式子表达的，可以判断真假的陈述句称为命题；
2、真命题、假命题：判断为真的语句称为真命题，判断为假的语句称为假命题。


注意：

1、并不是所有的语句都是命题，只有能够判断真假的语句才是命题。

2、如果一个语句是命题，则它是真命题或是假命题，二者必具其一。


基本不等式：

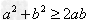（当且仅当a＝b时取“=”号）；
变式：①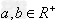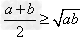，（当且仅当a＝b时取“=”号），即两个正数的算术平均不小于它们的几何平均。
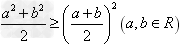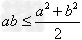②；③；④；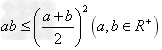


对基本不等式的理解：

(1)基本不等式的证明是利用重要不等式推导的，即，即有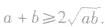
(2)基本不等式又称为均值定理、均值不等式等，其中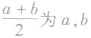的算术平均数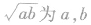，的几何平均数，本定理也可叙述为：两个正数的算术平均数不小于它们的几何平均数．
(3)要特别注意不等式成立的条件和等号成立的条件．均值不等式中：①当a=b时取等号，即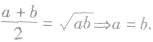


对于两个正数x，y，若已知xy，x+y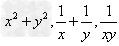，中的某一个为定值，可求出其余各个的最值：
如：（1）当xy＝P（定值），那么当x=y时，和x+y有最小值2，；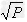
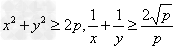（2）x+y=S（定值），那么当x=y时，积xy有最大值，；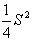
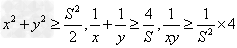（3）已知x2+y2=p，则x+y有最大值为，。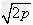

应用基本的不等式解题时：

注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”。

利用基本不等式比较实数大小：

(1)注意均值不等式的前提条件．
(2)通过加减项的方法配凑成使用均值定理的形式．
(3)注意“1”的代换．
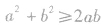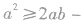
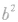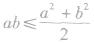(4)灵活变换基本不等式的形式，并注重其变形形式的运用．重要不等式的形式可以是，也可以是，还可以是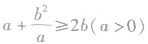等，不仅要掌握原来的形式，还要掌握它的几种变形形式以及公式的逆用等，以便应用．
(5)合理配组，反复应用均值不等式。 


基本不等式的几种变形公式：
 
 

发现相似题
与“下列说法正确的是（ ）A．a，b∈R，且a＞b，则a2＞b2B．若a＞b...”考查相似的试题有：