本试题 “如图,PA⊥平面ABCD,ABCD为正方形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。(1)求证:面EFG⊥面PAB;(2)求异面直线EG与BD所成的角的余弦值;(3)...” 主要考查您对异面直线所成的角
点到直线、平面的距离
平面与平面垂直的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 异面直线所成的角
- 点到直线、平面的距离
- 平面与平面垂直的判定与性质
异面直线所成角的定义:
直线a、b是异面直线,经过空间任意一点O,分别引直线a′∥a,b′∥b,则把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角,如下图。
两条异面直线所成角的范围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
在异面直线所成角定义中,空间一点O是任取的,而和点O的位置无关。 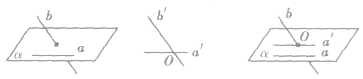
求异面直线所成角的步骤:
A、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选在特殊的位置上。
B、证明作出的角即为所求角;
C、利用三角形来求角。
特别提醒:
(1)两异面直线所成的角与点O(两直线平移后的交点)的选取无关.
(2)两异面直线所成角θ的取值范围是00<θ≤900.
(3)判定空间两条直线是异面直线的方法①判定定理:平面外一点A与平面内一点B的连线和平面内不过点B的直线是异面直线;②反证法:证明两直线共面不可能.
线线角的求法:
(1)定义法:用“平移转化”,使之成为两相交直线所成的角,当异面直线垂直时,应用线面垂直定义或三垂线定理及逆定理判定所成的角为900.
(2)向量法:设两条直线所成的角为θ(锐角),直线l1和l2的方向向量分别为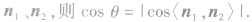
点到直线的距离:
由点向直线引垂线,这一点到垂足之间的距离。
点到平面的距离:
由点向平面引垂线,这点到垂足之间的距离,就叫做点到平面的距离。
求点面距离常用的方法:
(1)直接利用定义
①找到(或作出)表示距离的线段;
②抓住线段(所求距离)所在三角形解之.
(2)利用两平面互相垂直的性质如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离.
(3)体积法其步骤是:①在平面内选取适当三点和已知点构成三棱锥;②求出此三棱锥的体积V和所取三点构成三角形的面积S;③由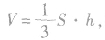 求出
求出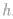 .这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
.这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
(4)转化法:将点到平面的距离转化为直线与平面的距离来求.
(5)向量法:

平面和平面垂直的定义:
如果两个平面相交,所成的二面角(从一条直线出发的两个半平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直。如图,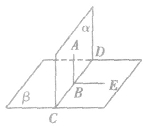
面面垂直的判定定理:
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。(线面垂直 面面垂直)
面面垂直)
面面垂直的性质定理:
如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。(面面垂直 线面垂直)
线面垂直)
性质定理符号表示:
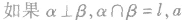

线线垂直、线面垂直、面面垂直的转化关系:
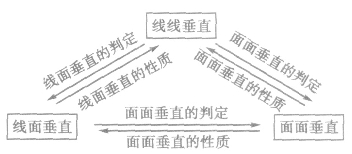
证明面面垂直的方法:
证明两个平面垂直,通常是通过证明线线垂直、线面垂直来实现的,在关于垂直问题的论证中要注意三者之间的相互转化,必要时可添加辅助线,如:已知面面垂直时,一般用性质定理,在一个平面内作出交线的垂线,使之转化为线面垂直,然后转化为线线垂直,故要熟练掌握三者之间的转化条件及常用方法.线面垂直与面面垂直最终归纳为线线垂直,证共面的两直线垂直常用勾股定理的逆定理、等腰三角形的性质;证不共面的两直线垂直通常利用线面垂直或利用空间向量.
常用结论:
(1)如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内,此结论可以作为性质定理用,
(2)从该性质定理的条件看出:只要在其中一个平面内通过一点作另一个平面的垂线,那么这条垂线必在这个平面内,点的位置既可以在交线上,也可以不在交线上,如图.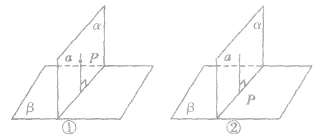
与“如图,PA⊥平面ABCD,ABCD为正方形,且PA=AD=2,E、F、G分别是...”考查相似的试题有:
- 已知二面角α-l-β的大小为60°,m、n为异面直线,且m⊥α,n⊥β,则m、n所成的角为[ ]A.30°B.60°C.90°D.120°
- 在直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M是CC1的中点,Q是BC的中点,点P在A1B1上,则直线PQ与直线AM所成的角等于( )A...
- 如图,将Rt△ABC沿斜边上的高AD折成1200的二面角C-AD-,若直角边AB=,AC=,则二面角A-B-D的正切值为( )A.B.C.D.1
- 已知平面,是内不同于的直线,那么下列命题中错误的是 A.若,则 B.若,则C.若,则 D.若,则
- 在如图所示的几何体中,四边形是矩形,平面,,∥,,,分别是,的中点.(1)求证:∥平面;(2)求证:平面.
- 在体积的球的表面上有A,B,C三点,AB=1,BC=,A,C两点的球面距离为,则球心到平面ABC的距离为( )。
- 如图,矩形ABCD中,AB=6,BC=2,沿对角线BD将△ABD向上折起,使点A移至点P,且点P在平面BCD内的投影O在CD上.(1) 求二面角P...
- 如图在棱长为a的正方体ABCD-A1B1C1D1中,过A1C1B的平面与底面ABCD的交线为l,则直线l与A1C1的距离为______.
- 如图,是边长为2的正方形,平面,,,且.(1)求证:平面;(2)求证:平面平面;(3)求多面体的体积。
- 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角...