椭圆的第一定义：

平面内与两个定点为F₁，F₂的距离的和等于常数（大于）的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。特别地，当常数等于时，轨迹是线段F₁F₂，当常数小于时，无轨迹。

椭圆的第二定义：

平面内到定点F的距离和到定直线l的距离之比等于常数e（0＜e＜1）的点的轨迹，叫做椭圆，定点F叫椭圆的焦点，定直线l叫做椭圆的准线，e叫椭圆的离心率。

椭圆的定义应该包含几个要素：

当题目中出现一点在椭圆上的条件时，注意使用定义

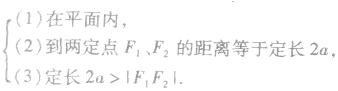
 椭圆的离心率：

椭圆的焦距与长轴长之比叫做椭圆的离心率。

椭圆的性质：

1、顶点：A（a，0），B（-a，0），C（0，b）和D（0，-b）。
2、轴：对称轴：x轴，y轴；长轴长|AB|=2a，短轴长|CD|=2b，a为长半轴长，b为短半轴长。
3、焦点：F₁（-c，0），F₂（c，0）。
4、焦距：。
5、离心率：；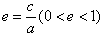 
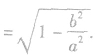
离心率对椭圆形状的影响：e越接近1，c就越接近a，从而b就越小，椭圆就越扁；e越接近0，c就越接近0，从而b就越大，椭圆就越圆；
6、椭圆的范围和对称性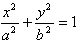：（a＞b＞0）中-a≤x≤a，-b≤y≤b，对称中心是原点，对称轴是坐标轴。
。

利用椭圆的几何性质解题：

利用椭圆的几何性质可以求离心率及椭圆的标准方程．要熟练掌握将椭圆中的某些线段长用a，b，c表示出来，例如焦点与各顶点所连线段的长，过焦点与长轴垂直的弦长等，这将有利于提高解题能力。

椭圆中求最值的方法：

求最值有两种方法：
(1)利用函数最值的探求方法利用函数最值的探求方法，将其转化为函数的最值问题来处理．此时应充分注意椭圆中x，y的范围，常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义，寻找图形中的几何元素、几何量之间的关系．

椭圆中离心率的求法：

在求离心率时关键是从题目条件中找到关于a，b，c的两个方程或从题目中得到的图形中找到a，b，c的关系式，从而求离心率或离心率的取值范围．