本试题 “已知|a|=2|b|≠0,且关于x的函数f(x)=13x3+12|a|x2+a•bx在R上有极值,则.a与.b的夹角范围为( )A.(0,π6)B.(π6,π]C.(π3,π]D.(π3,2π3]” 主要考查您对函数的单调性与导数的关系
用数量积表示两个向量的夹角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性与导数的关系
- 用数量积表示两个向量的夹角
导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间。
利用导数求解多项式函数单调性的一般步骤:
①确定f(x)的定义域;
②计算导数f′(x);
③求出f′(x)=0的根;
④用f′(x)=0的根将f(x)的定义域分成若干个区间,列表考察这若干个区间内f′(x)的符号,进而确定f(x)的单调区间:f′(x)>0,则f(x)在对应区间上是增函数,对应区间为增区间;f′(x)<0,则f(x)在对应区间上是减函数,对应区间为减区间。
函数的导数和函数的单调性关系特别提醒:
若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件,而不是必要条件。
用数量积表示两个向量的夹角:
设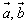 都是非零向量,
都是非零向量,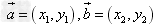 ,θ是
,θ是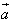 与
与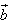 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得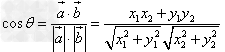 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
发现相似题
与“已知|a|=2|b|≠0,且关于x的函数f(x)=13x3+12|a|x2+a•bx在R上...”考查相似的试题有:
- 函数的递减区间为( )A.B.C.D.
- 已知函数f(x)=(x3-6x2+3x+t)ex,t∈R.依次在x=a,x=b,x=c(a<b<c)处取得极值.(Ⅰ)求t的取值范围;(Ⅱ)若a,b,c成...
- 已知函数在x=1处取得极值,求函数f(x)的单调区间.
- 已知函数f(x)=x2+alnx(a为常数).(1)若a=-4,讨论f(x)的单调性;(2)若a≥-4,求f(x)在[1,e]上的最小值及相应的x...
- 已知函数f(x)=-x3+3x2+9x+a,(Ⅰ)求f(x)的单调递减区间;(Ⅱ)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的...
- 设函数f(x)=ln(x-1)+2ax(a∈R)(1)求函数f(x)的单调区间;(2)如果当x>1,且x≠2时,ln(x-1)x-2>ax恒成立,则求实数a的取...
- 若函数f(x)=3ax-2a+1在区间[-1,1]上没有零点,则函数g(x)=(a+1)·(x3-3x+4) 的递减区间是( )。
- 下列函数在其定义域内是单调递增函数的是( )A.f(x)=x3-3xB.f(x)=3x-sinxC.f(x)=ex-xD.f(x)=lnx-x
- 设f(x)=px-px-2lnx.(Ⅰ)若f(x)在其定义域内为单调递增函数,求实数p的取值范围;(Ⅱ)设g(x)=2ex,且p>0,若在[1,e...
- 若|b|=2|a|≠0,c=a+b,且c⊥a,则向量a与b的夹角为______.