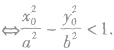等差数列的定义：
一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做公差，用符号语言表示为an+1-an=d。
等差数列的性质：
（1）若公差d＞0，则为递增等差数列；若公差d＜0，则为递减等差数列；若公差d＝0，则为常数列；
（2）有穷等差数列中，与首末两端“等距离”的两项和相等，并且等于首末两项之和；
（3）m，n∈N*，则am＝an+(m-n)d；
（4）若s，t，p，q∈N*，且s+t=p+q，则as+at=ap+aq，其中as，at，ap，aq是数列中的项，特别地，当s+t=2p时，有as+at=2ap；
（5）若数列｛an｝，｛bn｝均是等差数列，则数列｛man+kbn｝仍为等差数列，其中m，k均为常数。
（6）
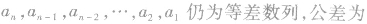
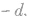
（7）从第二项开始起，每一项是与它相邻两项的等差中项，也是与它等距离的前后两项的等差中项，即
（8）
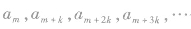仍为等差数列，公差为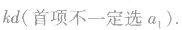
对等差数列定义的理解：
①如果一个数列不是从第2项起，而是从第3项或某一项起，每一项与它前一项的差是同一个常数，那么此数列不是等差数列，但可以说从第2项或某项开始是等差数列．
②求公差d时，因为d是这个数列的后一项与前一项的差，故有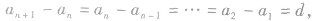
还有
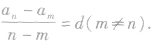
③公差d∈R，当d=0时，数列为常数列（也是等差数列）；当d>0时，数列为递增数列；当d<0时，数列为递减数列；
④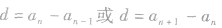
是证明或判断一个数列是否为等差数列的依据；
⑤证明一个数列是等差数列，只需证明an+1-an是一个与n无关的常数即可。
等差数列求解与证明的基本方法：
(1)学会运用函数与方程思想解题；
(2)抓住首项与公差是解决等差数列问题的关键；
(3)等差数列的通项公式、前n项和公式涉及五个量：a1，d，n，an，Sn，知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’)．
等比数列的定义：
一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做公比，公比通常用字母q表示（q≠0）。
等比数列的性质：
在等比数列｛an｝中，有
（1）若m+n=p+q，m，n，p，q∈N*，则aman=apaq；当m+n=2p时，aman=ap2；
（2）若m，n∈N*，则am=anqm-n；
（3）若公比为q，则｛
｝是以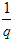
为公比的等比数列；
（4）下标成等差数列的项构成等比数列；
（5）
1）若a1＞0，q＞1，则｛an｝为递增数列；
2）a1＜0，q＞1， 则｛an｝为递减数列；
3）a1＞0，0＜q＜1，则｛an｝为递减数列；
4）a1＜0， 0＜q＜1， 则｛an｝为递增数列；
5）q＜0，则｛an｝为摆动数列；若q＝1，则｛an｝为常数列。
等差数列和等比数列的比较：
如何证明一个数列是等比数列：
证明一个数列是等比数列，只需证明
是一个与n无关的常数即可（或an2=an-1an+1）。
双曲线的离心率的定义：
(1)定义：双曲线的焦距与实轴长的比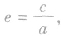
叫做双曲线的离心率．
(2)e的范围：e>l．
(3)e的含义：e是表示双曲线开口大小的一个量，e越大开口越大．
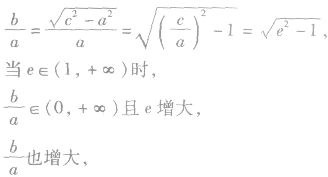
渐近线与实轴的夹角也增大。
双曲线的性质：
1、焦点在x轴上：顶点：（a，0），（-a，0）；焦点：（c，0），（-c，0）；
渐近线方程：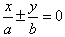
或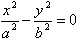
。
2、焦点在y轴上：顶点：（0，-a），（0，a）；焦点：（0，c），（0，-c）；
渐近线方程：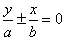
或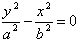
。
3、轴：x、y为对称轴，实轴长为2a，虚轴长为2b，焦距2c。
4、离心率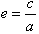
；
5、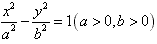
中，取值范围：x≤-a或x≥a，y∈R，对称轴是坐标轴，对称中心是原点。
双曲线的焦半径：
双曲线上的点
之间的线段长度称作焦半径，分别记作
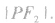
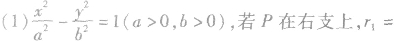
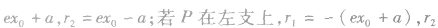
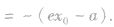
关于双曲线的几个重要结论：
(1)弦长公式（与椭圆弦长公式相同）．
(2)焦点三角形：已知
的两个焦点，P为双曲线上一点（异于顶点），
的面积为
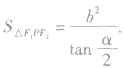
在解决与焦点三角形有关的问题时，应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用，还应注意灵活地运用平面几何、三角函数等知识来分析解决问题．
(3)基础三角形：如图所示，△AOB中，
(4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长．
(5)自双曲线的焦点作渐近线的垂线，垂足必在相应的准线上，即过焦点所作的渐近线的垂线，渐近线及相应准线三线共点．
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切．
(7)双曲线
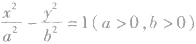
上一点P(x
0，y
0)处的切线方程是
(8)双曲线划分平面区域:对于双曲线
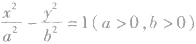
,我们有：P(x
0，y
0)在双曲线内部（与焦点共区域)
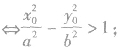
P(x
0，y
0)在双曲线外部（与焦点不其区域)
