两角和与差的公式:
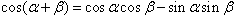
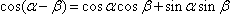
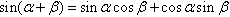
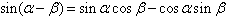
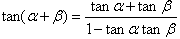
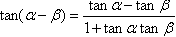
倍角公式:
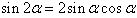
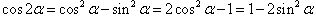
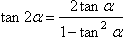
半角公式:
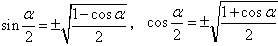
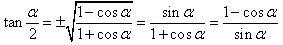
万能公式:
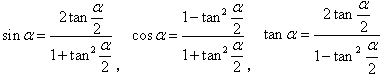
三角函数的积化和差与和差化积:
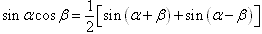

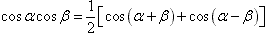
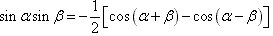
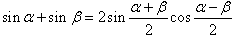
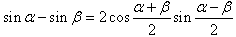
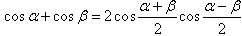
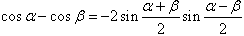
三角恒等变换:
寻找式子所包含的各个角之间的联系,并以此为依据选择可以联系它们的适当公式,这是三角恒等变换的特点。
三角函数式化简要遵循的"三看"原则:
(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.
(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.
(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.
方法提炼:
(1)解决给值求值问题的一般思路:
①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.
(2)解决给值求角问题的一般步骤:
①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.