本试题 “已知集合A={sinα,cosα,1},B={sin2α,sinα+cosα,0},且A=B,则sin2012α+cos2012α=______.” 主要考查您对集合间的基本关系
同角三角函数的基本关系式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合间的基本关系
- 同角三角函数的基本关系式
集合与集合的关系有“包含”与“不包含”,“相等”三种:
1、 子集概念:
一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,就说集合B包含A,记作A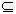 B(或说A包含于B),
B(或说A包含于B),
也可记为B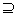 A(B包含A),此时说A是B的子集;A不是B的子集,记作A
A(B包含A),此时说A是B的子集;A不是B的子集,记作A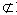 B,读作A不包含于B
B,读作A不包含于B
2、集合相等:
对于集合A和B,如果集合A中的每一个元素都是集合B的元素,反过来,集合B的每一个元素也都是集合A的元素,即集合A是集合B的子集,且集合B是集合A的子集,我么就说集合A和集合B相等,记作A=B
3、真子集:
对于集合A与B,如果A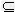 B并且A≠B,则集合A是集合B的真子集,记作A
B并且A≠B,则集合A是集合B的真子集,记作A B(B
B(B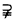 A),读作A真包含于B(B真包含A)
A),读作A真包含于B(B真包含A)
集合间基本关系:
性质1:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性:AB,BCAC;AB,BCAC;
(4)AB,BAA=B。
性质2:
子集个数的运算:含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
集合间基本关系性质:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性: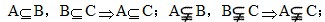
(4)集合相等:
(5)含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
同角三角函数的关系式:
(1)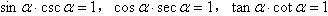 ;
;
(2)商数关系: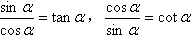 ;
;
(3)平方关系: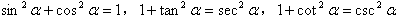 。
。
同角三角函数的基本关系的应用:
已知一个角的一种三角函数值,根据角的终边的位置利用同角三角函数的基本关系,可以求出这个角的其他三角函数值.
同角三角函数的基本关系的理解:
(1)在公式中,要求是同一个角,如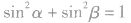 不一定成立.
不一定成立.
(2)上面的关系式都是对使它的两边具有意义的那些角而言的,如:基本三角关系式 。对一切α∈R成立;
。对一切α∈R成立;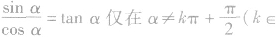 Z)时成立.
Z)时成立.
(3)同角三角函数的基本关系的应用极为为广泛,它们还有如下等价形式: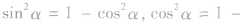

(4)在应用平方关系时,常用到平方根、算术平方根和绝对值的概念,应注意“±”的选取.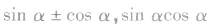 间的基本变形 三者通过
间的基本变形 三者通过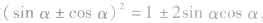 ,可知一求二,有关
,可知一求二,有关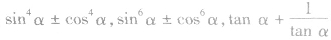 等化简都与此基本变形有广泛的联系,要熟练掌握。
等化简都与此基本变形有广泛的联系,要熟练掌握。
与“已知集合A={sinα,cosα,1},B={sin2α,sinα+cosα,0},且A=B...”考查相似的试题有:
- 对于集合A,B,我们把集合{x|x∈A},且x∉B叫做集合A与B的差集,记做A-B,若A-B=∅,则集合A与B之间的关系是______.
- 设集合A={x∈Q|x>1},则[ ]A.?AB.C.D.A
- 已知,则的值为( )A.B.C.D.
- 函数y=cos4x-sin4x的最小正周期是( )A.π2B.πC.2πD.4π
- 已知α是第二象限的角,tanα=-3,则sin(90°+α)=______.
- 已知,求和的值.
- 已知复数z1=cosα+isinα,z2=cosβ+isinβ,|z1-z2|=255.求:(1)求cos(α-β)的值;(2)若-π2<β<0<α<π2,且sinβ=-513,...
- ( )A.B.C.D.
- 求tan20°+4sin20°的值.
- 已知sinα+cosβ=13,sinβ-cosα=12,则sin(α-β)=______.