本试题 “已知△ABC的顶点坐标分别为A（1，1）、B（4，1）、C（4，5），则cosA=（ ）A．-45B．45C．-35D．35” 主要考查您对余弦定理
两点间的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 余弦定理
- 两点间的距离
余弦定理：
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍，
即
。
推论：
在△ABC中，若a2+b2=c2，则C为直角；若a2+b2＞c2，则C为锐角；若a2+b2＜c2，则C为钝角。
余弦定理在解三角形中的应用：
（1）已知两边和夹角，
（2）已知三边。
其它公式：
射影公式：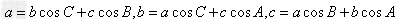
两点间的距离公式：
设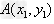
，
是平面直角坐标系中的两个点，则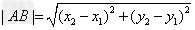
。
特别地，原点O（0,0）与任意一点P（x,y）的距离为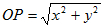
两点间的距离公式的理解：
（1）在公式中，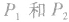
的位置是对称的，没有先后之分，即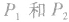间的距离也可表示为
（2）
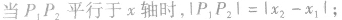
发现相似题
与“已知△ABC的顶点坐标分别为A（1，1）、B（4，1）、C（4，5），...”考查相似的试题有：
- 若的面积为，则角=__________.
- 角A、B、C分别是锐角△ABC的三边a、b、c所对的角，2a•sinC=3•c．（Ⅰ）求角A的大小；（Ⅱ）若△ABC的面积S=3，求a的最小值．
- a、b、c是△ABC的三边，求证a2+b2+c2＜2（ab+bc+ac）．
- 在△ABC中，角A，B，C所对的边分别为a，b，c，已知a=2，c=3，cosB=，（1）求b的值；（2）求sinC的值．
- 三角形三边长为，且满足等式,则边所对角为A． 150°B． 30°C． 60°D． 120° [
- 在三角形ABC中，AB=5，AC=3，BC=7，则∠BAC大小为[ ]A.B.C.D.
- 在△ABC中，a2+b2=c2+ab，且cosAcosB=，试判断△ABC的形状。
- 某货轮在A处看灯塔B在货轮北偏东75°，距离为12nmile；在A处看灯塔C在货轮的北偏西30°，距离为8nmile，货轮由A处向正北航行到D...
- 在△中，角所对的边分别为，已知，，．（1）求的值；（2）求的值．
- 点P（1，0）到曲线（其中参数t∈R）上的点的最短距离为（ ） A．0 B．1 C． D．2