本试题 “以下四个命题:①工厂制造的某机械零件尺寸ξ~N(4,),在一次正常的试验中,取1000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有3个.②抛掷n次硬币...” 主要考查您对函数的单调性、最值
函数的极限及四则运算
直线与双曲线的应用
正态分布
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性、最值
- 函数的极限及四则运算
- 直线与双曲线的应用
- 正态分布
单调性的定义:
1、对于给定区间D上的函数f(x),若对于任意x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),则称f(x)是区间上的增函数;当x1<x2时,都有f(x1)>f(x2),则称f(x)是区间D上的减函数。
2、如果函数y=f(x)在区间上是增函数或减函数,就说函数y=f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。如果函数y=f(x)在区间D上是增函数或减函数,区间D称为函数f(x)的单调增或减区间
3、最值的定义:
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最大值.
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最小值
判断函数f(x)在区间D上的单调性的方法:
(1)定义法:其步骤是:
①任取x1,x2∈D,且x1<x2;
②作差f(x1)-f(x2)或作商 ,并变形;
,并变形;
③判定f(x1)-f(x2)的符号,或比较 与1的大小;
与1的大小;
④根据定义作出结论。
(2)复合法:利用基本函数的单调性的复合。
(3)图象法:即观察函数在区间D上部分的图象从左往右看是上升的还是下降的。
函数极限的定义:
(1)当自变量n取正值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于正无穷大时,函数f(x)的极限是a,
记作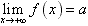 或当x→+∞是,f(x)→a;
或当x→+∞是,f(x)→a;
(2)当自变量n取负值并且绝对值无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于负无穷大时,函数f(x)的极限是a,记作 或当x→-∞是,f(x)→a;
或当x→-∞是,f(x)→a;
若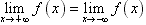 ,称x→∞时,f(x)的极限是a,
,称x→∞时,f(x)的极限是a,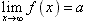 。
。
函数的左极限:
当x从x=x0点的左侧(即x<x0)无限地接近于x0时,f(x)无限趋近于一个常数a,则称a是f(x)在点x0 处的左极限,记作 ;
;
函数的右极限:
当x从x=x0点的右侧(即x>x0)无限地接近于x0时,f(x)无限趋近于一个常数a,则称a是f(x)在点x0处的右极限,记作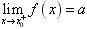 。
。
f(x)在点x0处的极限:
当x无限地接近于x0(可由任何方向接近)时,f(x)无限趋近于一个常数a,则称a是f(x)在点x0处的极限, 。
。
函数极限的运算法则:
若f(x)=C(C为常数),则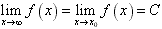 ;
;
若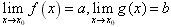 ,则
,则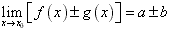 ;
; 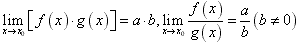 。
。
直线与双曲线:
设直线l的方程为:Ax+By+C=0(A、B不同时为零),双曲线的方程: ,将直线的方程代入双曲线的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
,将直线的方程代入双曲线的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
双曲线的综合问题:
双曲线知识通常与圆、椭圆、抛物线或数列、向量及不等式、三角函数相联系,综合考查数学知识及应用是高考的重点,应用中应注意对知识的综合及分析能力,双曲线的标准方程和几何性质中涉及很多基本量,如“a,b,c,e"树立基本量思想对于确定双曲线方程和认识其几何性质有很大帮助.另外,渐近线是双曲线特有的,双曲线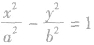 的渐近线方程可记为
的渐近线方程可记为
 为渐近线的双曲线方程可设为
为渐近线的双曲线方程可设为 .特别地,等轴双曲线方程可设为
.特别地,等轴双曲线方程可设为
 的垂直关系的证明可以通过
的垂直关系的证明可以通过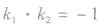 来证明,也可以通过
来证明,也可以通过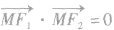 来证明,它体现了证明解析几何问题方法的多样性.
来证明,它体现了证明解析几何问题方法的多样性.正态分布的定义:
如果随机变量ξ的总体密度曲线是由或近似地由下面的函数给定: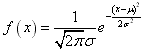 ,x∈R,则称ξ服从正态分布,这时的总体分布叫正态分布,其中μ表示总体平均数,σ叫标准差,正态分布常用
,x∈R,则称ξ服从正态分布,这时的总体分布叫正态分布,其中μ表示总体平均数,σ叫标准差,正态分布常用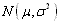 来表示。
来表示。
当μ=0,σ=1时,称ξ服从标准正态分布,这时的总体叫标准正态总体。 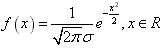 叫标准正态曲线。
叫标准正态曲线。
正态曲线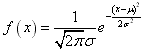 ,x∈R的有关性质:
,x∈R的有关性质:
(1)曲线在x轴上方,与x轴永不相交;
(2)曲线关于直线x=μ对称,且在x=μ两旁延伸时无限接近x轴;
(3)曲线在x=μ处达到最高点;
(4)当μ一定时,曲线形状由σ的大小来决定,σ越大,曲线越“矮胖”,表示总体分布比较离散,σ越小,曲线越“瘦高”,表示总体分布比较集中。
在标准正态总体N(0,1)中:
(1)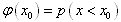 ;
;
(2)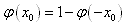 (因为曲线关于y轴对称);
(因为曲线关于y轴对称);
(3) ,
,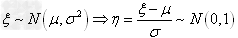 。
。
与“以下四个命题:①工厂制造的某机械零件尺寸ξ~N(4,),在一...”考查相似的试题有:
- 定义在R上的函数y=f(x)在(-∞,a)上是增函数,且函数y=f(x+a)的偶函数,则当x1<a<x2且|x1-a|<|x2-a|时,有( )A.f...
- 已知g(x)=mx+2,f(x)=x2-,若对任意的x1∈[-1,2],总存在x2∈[1,],使得g(x1)>f(x2),则m的取值范围是[ ]A.{0}B.C...
- 函数在区间上是递减的,则实数k的取值范围为 .
- 已知f(x)=f(x+1),(-2<x<0)2x+1,(0≤x<2)x2-1,(x≥2)(1)若f(a)=4,且a>0,求实数a的值.(2)求f(-32)的值.
- 设(a,b),(c,d)都是函数f(x)的单调增区间,且x1∈(a,b),x2∈(c,d),x1<x2,则f(x1)与f(x2)的大小关系是[ ]A.f(x1)<f(x2...
- 定义在(-1,1)上的奇函数f(x)是减函数,且f(1-a)+f(1-a2)<0,求实数a的取值范围.
- 函数y=log2(2x-x2)的单调递增区间是______.
- 函数y=2x2-3x+1的单调递减区间为 ______.
- 已知函数f(x)=|1x-1|(1)判断f(x)在[1,+∞)上的单调性,并证明你的结论;(2)若集合A={y|y=f(x),12≤x≤2},B=[0,1],...
- 某市进行一次高三教学质量抽样检测,考试后统计的所有考生的数学成绩服从正态分布.已知数学成绩平均分为90分,60分以下的人...