返回

高中数学

首页
首页 高中数学知识 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等） 余弦定理 试题正文
  • 解答题
    △ABC中，角A，B，C对边的边长分别是a，b，c，且a（cosB+cosC）=b+c．
    （1）求证：A=
    π
    2
    ；
    （2）若△ABC外接圆半径为1，求△ABC周长的取值范围．
    本题信息：数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “△ABC中，角A，B，C对边的边长分别是a，b，c，且a（cosB+cosC）=b+c．（1）求证：A=π2；（2）若△ABC外接圆半径为1，求△ABC周长的取值范围．” 主要考查您对

正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）

余弦定理

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）
  • 余弦定理

正弦函数和余弦函数的图象：正弦函数y=sinx（x∈R）和余弦函数y=cosx（x∈R）的图象分别叫做正弦曲线和余弦曲线，

1．正弦函数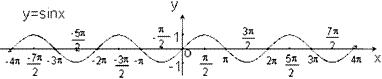

2．余弦函数

函数图像的性质
正弦、余弦函数图象的性质：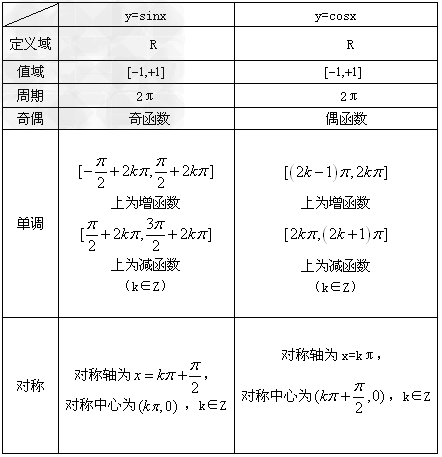

由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当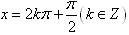时，y取最大值1，
当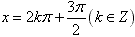时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。




正弦、余弦函数图象的性质：


由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当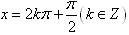时，y取最大值1，
当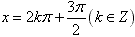时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。



余弦定理：

三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍，
即。

推论：

在△ABC中，若a2+b2=c2，则C为直角；若a2+b2＞c2，则C为锐角；若a2+b2＜c2，则C为钝角。


余弦定理在解三角形中的应用：

（1）已知两边和夹角，
（2）已知三边。


其它公式：

射影公式：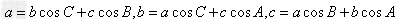


发现相似题
与“△ABC中，角A，B，C对边的边长分别是a，b，c，且a（cosB+cosC...”考查相似的试题有：