本试题 “已知平面向量a=(3,-1),b=(12,32).(I)若存在实数k和t,使得x=a+(t2-3)b,y=-ka+b,且x⊥y,试求函数的关系式k=f(t);(II)根据(I)结论,确定k...” 主要考查您对函数的单调性与导数的关系
用数量积判断两个向量的垂直关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性与导数的关系
- 用数量积判断两个向量的垂直关系
导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间。
利用导数求解多项式函数单调性的一般步骤:
①确定f(x)的定义域;
②计算导数f′(x);
③求出f′(x)=0的根;
④用f′(x)=0的根将f(x)的定义域分成若干个区间,列表考察这若干个区间内f′(x)的符号,进而确定f(x)的单调区间:f′(x)>0,则f(x)在对应区间上是增函数,对应区间为增区间;f′(x)<0,则f(x)在对应区间上是减函数,对应区间为减区间。
函数的导数和函数的单调性关系特别提醒:
若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件,而不是必要条件。
两向量垂直的充要条件:
非零向量 ,那么
,那么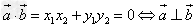 ,所以可以根据此公式判断两个向量是否垂直。
,所以可以根据此公式判断两个向量是否垂直。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“已知平面向量a=(3,-1),b=(12,32).(I)若存在实数k和...”考查相似的试题有:
- 若曲线在点处的切线与两条坐标轴围成的三角形的面积为54,则( )A.3B.6C.9D.18
- 已知函数f(x)=xx2+b,其中b∈R.(Ⅰ)若x=-1是f(x)的一个极值点,求b的值;(Ⅱ)求f(x)的单调区间.
- (本小题14分)设函数,曲线过P(1,0),且在P点处的切斜线率为2.(I)求a,b的值;(II)证明:.
- 已知函数f(x)=(ax2-2x)e-x(a∈R).(1)当a≥0时,求f(x)的极值点;(2)设f(x)在[-1,1]上是单调函数,求出a的取值...
- 已知函数f(x)=13x3+12ax2+x+b(a≥0),f′(x)为函数f(x)的导函数.(Ⅰ)设函数f(x)的图象与x轴交点为A,曲线y=f(x)...
- 已知函数f(x)=-13x3+bx2-3a2x(a≠0)在x=a处取得极值.(Ⅰ)求ba;(Ⅱ)设函数g(x)=2x3-3af′(x)-6a3,如果g(x)在开区间(...
- 若函数f(x)=x3+ax2+bx+c在区间[-1,0]上是单调递减函数,则a2+b2的最小值为( )。
- (普通班做) 设函数f(x)=lnx+x2+ax.若f(x)在其定义域内为增函数,则a的取值范围为______.
- 给定三个向量=(1,0,1),=(1,1,0),=(1,1,k2+k-1),其中k是一个实数,若存在非零向量同时垂直这三个向量,则k的取值为(...
- 如果=,≠那么( ) A.= B.=λ C.⊥ D.,在上的投影相等