返回

高中数学

首页
首页 高中数学知识 集合间交、并、补的运算（用Venn图表示） 指数函数的解析式及定义（定义域、值域） 对数函数的解析式及定义（定义域、值域） 试题正文
  • 解答题
    已知集合U=R，A={x|y=
    		log2(x-1)
     }    ，B={y|y=(
    1
    2
    )    x    +1，-2≤x≤-1 }
    （1）求集合A、B；  （2）求A∩B、A∩（CUB）．
    本题信息：数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “已知集合U=R，A={x|y=log2(x-1) }，B={y|y=(12)x+1，-2≤x≤-1 }（1）求集合A、B； （2）求A∩B、A∩（CUB）．” 主要考查您对

集合间交、并、补的运算（用Venn图表示）

指数函数的解析式及定义（定义域、值域）

对数函数的解析式及定义（定义域、值域）

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 集合间交、并、补的运算（用Venn图表示）
  • 指数函数的解析式及定义（定义域、值域）
  • 对数函数的解析式及定义（定义域、值域）

1、交集概念：

（1）一般地，由所有属于集合A且集合B的元素所组成的集合，叫做A与B的交集，记作A∩B，读作A交B，表达式为A∩B＝｛x|x∈A且x∈B｝。
（2)韦恩图表示为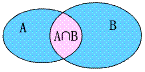
。


2、并集概念：


（1）一般地，由所有属于集合A或集合B的元素所组成的集合，叫做A与B的并集，记作A∪B，读作A并B，表达式为A∪B＝｛x|x∈A或x∈B｝。
（2）韦恩图表示为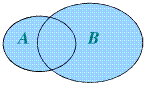
。


3、全集、补集概念：


（1）全集：一般地，如果一个集合含有我们所要研究的各个集合的全部元素，就称这个集合为全集，通常记作U。
        补集：对于一个集合A，由全集U中所有不属于A的元素组成的集合称为集合A相对于全集U的补集，记作CUA，读作U中A的补集，表达式为CUA={x|x∈U，且x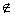A}。
（2）韦恩图表示为
。


1、交集的性质：

 

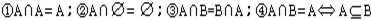
2、并集的性质：

 

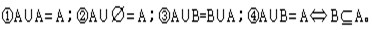
3、补集的性质：

 


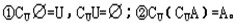
指数函数的定义：

一般地，函数y=ax（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R，值域是（0，+∞）。

指数函数的解析式：

y=ax（a＞0，且a≠1）


 理解指数函数定义，需注意的几个问题：

①因为a>0，x是任意一个实数时，ax是一个确定的实数，所以函数的定义域为实数集R．
②规定底数a大于零且不等于1的理由：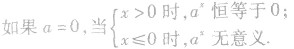

如果a<0，比如y=(-4)x，这时对于在实数范围内函数值不存在．
如果a=1，y=1x=1是一个常量，对它就没有研究的必要，
为了避免上述各种情况，所以规定a>0且a≠1．
③像等函数都不是指数函数，要注意区分。


对数函数的定义：

一般地，我们把函数y=logax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R。

对数函数的解析式：

y=logax（a＞0，且a≠1）


在解有关对数函数的解析式时注意：

在涉及到对数函数时，一定要注意定义域，即满足真数大于零；求值域时，还要考虑底数的取值范围。


发现相似题
与“已知集合U=R，A={x|y=log2(x-1) }，B={y|y=(12)x+1，-2≤x≤-1 ...”考查相似的试题有：