本试题 “函数的定义域是( )” 主要考查您对函数的定义域、值域
函数的零点与方程根的联系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
- 函数的零点与方程根的联系
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则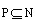 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如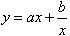 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
函数零点的定义:
一般地,如果函数y =f(x)在实数a处的值等于零,即f(a)=o,则a叫做这个函数的零点,有时我们把一个函数的图象与x轴的交点的横坐标,也叫做这个函数的零点。
函数零点具有的性质:
对于任意函数y=(x)只要它的图象是连续不间断的,则有:
(1)当它通过零点时(不是二重零点),函数值变号.如函数f(x)=x2-2x -3的图象在零点-1的左边时,函数值取正号,当它通过第一个零点-1时,函数值由正变为负,在通过第二个零点3时,函数值又由负变为正.
(2)在相邻两个零点之间所有的函数值保持同号,
方程的根与函数的零点的联系:
方程f(x)=0有实根 函数y=f(x)的图像与x轴有交点
函数y=f(x)的图像与x轴有交点 函数y=f(x)有零点
函数y=f(x)有零点
与“函数的定义域是( )”考查相似的试题有:
- 函数的值域是[ ]A.(-∞,-1)B.(-∞,0)∪(0,+∞)C.(-1,+∞)D.(-∞,-1) ∪(0,+∞)
- 函数的定义域为( )A.B.RC.{x |}D.x=1
- 设函数f(x)=eXx2+ax+a,其中a为实数.(Ⅰ)若f(x)的定义域为R,求a的取值范围;(Ⅱ)当f(x)的定义域为R时,求f(x)的...
- 函数y=1+x的定义域是( )A.[-1,+∞)B.{x|x≥-1,且x≠0}C.(-1,+∞)D.(-∞,-1)
- 已知函数f(x)=x+1-aa-x(a∈R且x≠a),当f(x)的定义域为[a+13,a+12]时,求f(x)的值域.
- 若方程在区间且上有一根,则a的值为 A.1B.2C.3D.4
- 方程log2(x+4)=3x的实数解个数为( ) A.0 B.1 C.2 D.3
- 如果函数y=|x|-2的图象与曲线C:x2+y2=λ恰好有两个不同的公共点,则实数λ的取值范围为______.
- 已知函数,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,(Ⅰ)求函数y=f(x)的不动点;(Ⅱ)已知a、b是y=f(x)...
- 函数f(x)=的图象如图所示,则a+b+c=________.