返回

高中数学

首页
首页 高中数学知识 函数的零点与方程根的联系 两角和与差的三角函数及三角恒等变换 试题正文
  • 单选题
    已知方程
    |sinx|
    x
    =k    在（0，+∞）有两个不同的解α，β（α＜β），则下面结论正确的是（　　）
    A．tan(α+
    π
    4
    )=
    1+α
    1-α
    		B．tan(α+
    π
    4
    )=
    1-α
    1+α
    C．tan(β+
    π
    4
    )=
    1+β
    1-β
    		D．tan(β+
    π
    4
    )=
    1-β
    1+β

    本题信息：2013年揭阳一模数学单选题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “已知方程|sinx|x=k在（0，+∞）有两个不同的解α，β（α＜β），则下面结论正确的是（ ）A．tan(α+π4)=1+α1-αB．tan(α+π4)=1-α1+αC．tan(β+π4)=1+β1-βD．tan(β+π4...” 主要考查您对

函数的零点与方程根的联系

两角和与差的三角函数及三角恒等变换

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 函数的零点与方程根的联系
  • 两角和与差的三角函数及三角恒等变换

函数零点的定义：

一般地，如果函数y =f(x)在实数a处的值等于零，即f(a)=o，则a叫做这个函数的零点，有时我们把一个函数的图象与x轴的交点的横坐标，也叫做这个函数的零点。               


函数零点具有的性质：

对于任意函数y=(x)只要它的图象是连续不间断的，则有：
(1)当它通过零点时（不是二重零点），函数值变号．如函数f(x)=x2-2x -3的图象在零点-1的左边时，函数值取正号，当它通过第一个零点-1时，函数值由正变为负，在通过第二个零点3时，函数值又由负变为正．
(2)在相邻两个零点之间所有的函数值保持同号，


方程的根与函数的零点的联系：

方程f（x）=0有实根函数y=f（x）的图像与x轴有交点函数y=f（x）有零点


两角和与差的公式：






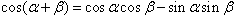
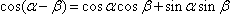
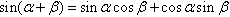
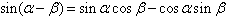
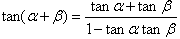
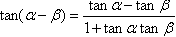
倍角公式：



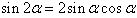
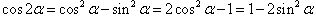
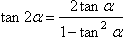
半角公式：


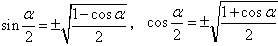
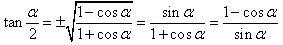
万能公式：

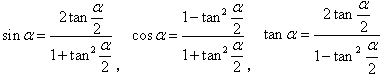
三角函数的积化和差与和差化积：








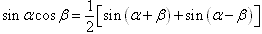
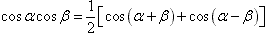
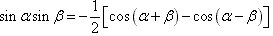
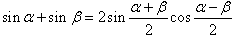
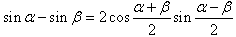
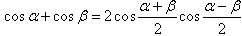
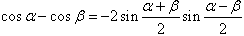
三角恒等变换：

寻找式子所包含的各个角之间的联系，并以此为依据选择可以联系它们的适当公式，这是三角恒等变换的特点。


三角函数式化简要遵循的"三看"原则:

(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.
(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.
(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.

方法提炼:

(1)解决给值求值问题的一般思路:
①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.
(2)解决给值求角问题的一般步骤:
①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.


发现相似题
与“已知方程|sinx|x=k在（0，+∞）有两个不同的解α，β（α＜β），...”考查相似的试题有：