返回

高中二年级数学

首页
首页 高中二年级数学知识 等比数列的定义及性质 向量数乘运算及几何意义 直线与抛物线的应用 试题正文
  • 解答题
    已知抛物线y2=4x，过点的直线l与抛物线交于A、B两点，且直线l与x轴交于点C.
    （1）求证:，，成等比数列；
    （2 ）设，，试问α+β是否为定值，若是，求出此定值；若不是，请说明理由．
    本题信息：2012年湖北省期中题数学解答题难度一般 来源:朱潇（高中数学）
  • 本题答案
    查看答案
本试题 “已知抛物线y2=4x，过点的直线l与抛物线交于A、B两点，且直线l与x轴交于点C.（1）求证:，，成等比数列；（2 ）设，，试问α+β是否为定值，若是，求出此定值；若...” 主要考查您对

等比数列的定义及性质

向量数乘运算及几何意义

直线与抛物线的应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 等比数列的定义及性质
  • 向量数乘运算及几何意义
  • 直线与抛物线的应用

等比数列的定义：

一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做公比，公比通常用字母q表示（q≠0）。


等比数列的性质：

在等比数列｛an｝中，有
（1）若m+n=p+q，m，n，p，q∈N*，则aman=apaq；当m+n=2p时，aman=ap2；
（2）若m，n∈N*，则am=anqm-n；
（3）若公比为q，则｛｝是以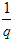为公比的等比数列；
（4）下标成等差数列的项构成等比数列；
（5）
1）若a1＞0，q＞1，则｛an｝为递增数列；
2）a1＜0，q＞1， 则｛an｝为递减数列；
3）a1＞0，0＜q＜1，则｛an｝为递减数列；
4）a1＜0， 0＜q＜1， 则｛an｝为递增数列；
5）q＜0，则｛an｝为摆动数列；若q＝1，则｛an｝为常数列。


等差数列和等比数列的比较：
 

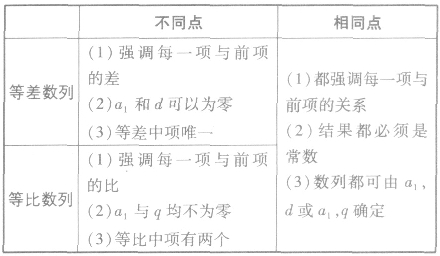
如何证明一个数列是等比数列：

证明一个数列是等比数列，只需证明是一个与n无关的常数即可（或an2=an-1an+1）。


向量的数乘的定义：

我们规定实数λ与向量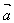的积是一个向量，记作λ；

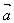向量的数乘的长度和方向规定如下：

（1）；
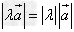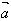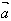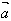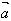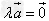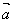（2）当λ＞0时，λ的方向与的方向相同；当λ＜0时，λ的方向与的方向相反；当λ＝0时，；注意：λ≠0

数乘运算的坐标表示：

设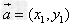，则。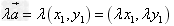


实数与向量积的运算律：

（1）；
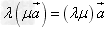（2）；
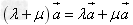（3）。


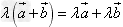向量数乘运算的理解：

①向量数乘运算结果仍然是向量．
②实数与向量的积的特殊情况：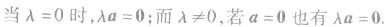
 
③实数与向量可以求积，但是不能进行加减运算，比如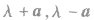无意义。
④由向量数乘的概念可知其几何意义，可以把向量a的长度扩大（当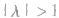时），也可以缩小（当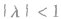时），同时，我们可以不改变向量a的方向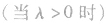，也可以改变向量a的方向（当λ<0时）。

 

设直线l的方程为：Ax+By+C=0（A、B不同时为零），抛物线的方程为y2=2px（p＞0），将直线的方程代入抛物线的方程，消去y（或x） 得到一元二次方程，进而应用根与系数的关系解题。

直线与抛物线的位置关系:

直线和抛物线的位置关系，可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定，同时注意过焦点的弦的一些性质，如：


发现相似题
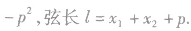
与“已知抛物线y2=4x，过点的直线l与抛物线交于A、B两点，且直线l...”考查相似的试题有：