函数零点的定义：

一般地，如果函数y =f(x)在实数a处的值等于零，即f(a)=o，则a叫做这个函数的零点，有时我们把一个函数的图象与x轴的交点的横坐标，也叫做这个函数的零点。               

函数零点具有的性质：

对于任意函数y=(x)只要它的图象是连续不间断的，则有：
(1)当它通过零点时（不是二重零点），函数值变号．如函数f(x)=x²-2x -3的图象在零点-1的左边时，函数值取正号，当它通过第一个零点-1时，函数值由正变为负，在通过第二个零点3时，函数值又由负变为正．
(2)在相邻两个零点之间所有的函数值保持同号，

方程的根与函数的零点的联系：

方程f（x）=0有实根函数y=f（x）的图像与x轴有交点函数y=f（x）有零点

绝对值不等式：

当a>0时，有；
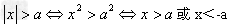或x＜-a 。

 
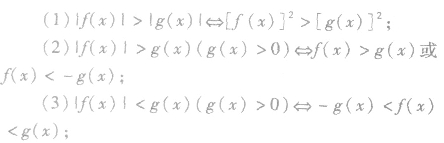
          (4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解，也可以用图象法求解。

回归直线：

如果散点图中点的分布从整体上看大致在一条直线附近，我们就称这两个变量之间具有线性相关关系，这条直线叫做回归直线；

最小二乘法：

使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法。

回归直线方程：

，
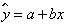其中。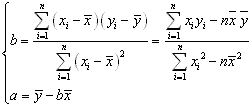

回归分析是处理变量相关关系的一种常用数学方法，其步骤为：

（1）确定特定量之间是否有相关关系，如果有，那么就找出他们之间贴近的数学表达式；
（2）根据一组观察值，预测变量的取值及判断变量取值的变化趋势；
（3）求出回归直线方程。