本试题 “已知以F为焦点的抛物线y2=4x上的两点A、B满足,则弦AB的中点到准线的距离为( )。” 主要考查您对直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线与抛物线的应用
设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
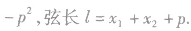
发现相似题
与“已知以F为焦点的抛物线y2=4x上的两点A、B满足,则弦AB的中点...”考查相似的试题有:
- 已知抛物线C:x2=2py(p>0)的焦点为F,定点A(3,2)与点F在C的两侧,C上的动点P到点A的距离与到其准线l的距离之和的最小值...
- 已知抛物线C:y2=4x,过点A(-1,0)的直线交抛物线C于P、Q两点,设AP=λAQ.(Ⅰ)若点P关于x轴的对称点为M,求证:直线MQ经过...
- 已知抛物线y=ax2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为______.
- 倾斜角为π4的直线l经过抛物线y2=4x的焦点,且与抛物线相交于A、B两点,求线段AB的长.
- 抛物线C的顶点在坐标原点,焦点在y轴的负半轴上,过点M(0,-2)作直线l与抛物线C交于A,B两点,且满足=(-4,-12)。(1)求...
- 过抛物线y2=4x上的焦点作斜率为1的直线,交抛物线于A、B两点,则|AB|的值为[ ]A.2B.3C.4D.8
- 已知以F为焦点的抛物线y2=4x上的两点A、B满足,则弦AB的中点到准线的距离为( )。
- 已知抛物线y2=2px(p>0)的焦点为F,准线为l.(1)求抛物线上任意一点Q到定点N(2p,0)的最近距离;(2)过点F作一直线与...
- 已知抛物线y2=4x,焦点为F,顶点为O,点P在抛物线上移动,Q是OP的中点.(1)求点Q的轨迹方程;(2)若倾斜角为60°且过点F的...
- 抛物线的顶点在原点,焦点在射线x﹣y+1=0(x≥0)上(1)求抛物线的标准方程(2)过(1)中抛物线的焦点F作动弦AB,过A、B两点...