本试题 “设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上的一个动点,与x轴正方向的夹角为60°,求||的值.” 主要考查您对向量模的计算
直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量模的计算
- 直线与抛物线的应用
向量的模:
设 ,则有向线段
,则有向线段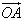 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: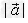 ,则
,则  。
。
向量模的坐标表示:
(1)若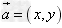 ,则
,则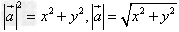 ;
;
(2)若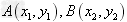 ,那么
,那么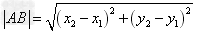 。
。
求向量的模:
求向量的模主要是利用公式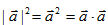 来解。
来解。
设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
发现相似题
与“设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上...”考查相似的试题有:
- 已知向量a与向量b的夹角为120°,若向量c=a+b,且a⊥c,则|a||b|的值为______.
- 已知向量a、b的夹角为60°,|a|=2,|b|=3,则|2a-b|=______.
- 已知在矩形ABCD中,AB=2,BC=3,则的模等于( ) A.4 B.5 C. D.2
- 已知向量=(sinθ,cosθ-2sinθ),=(1,2),(1)若,求tanθ的值;(2)若(0<θ<π),求θ的值;(3)设=(1,1+2sinθ),...
- 若平面向量,,两两所成的角相等,||=||=1,||=3,则|++|=( ) A.2 B.4 C.2或5 D.4或5
- 已知向量a=(cos3x2,sin3x2),b=(cosx2,-sinx2),x∈[-π3,π2](1)求证:(a-b)⊥(a+b);(2)|a+b|=13,求cosx的值.
- 如图,半径为1圆心角为圆弧上有一点C,(1)当C为圆弧中点时,D为线段OA上任一点,求的最小值;(2)当C在圆弧上运动时,D、E...
- 已知向量a=(cosα,sinα),b=(cosβ,sinβ).(1)求a•(a+2b)的取值范围;(2)若α-β=π3,求|a+2b|.
- 在平面直角坐标系xOy中,直线l过抛物线y2=4x的焦点F交抛物线于A、B两点,(1)若|AB|=8,求直线l的斜率;(2)若|AF|=m,|BF|...
- 若A、B是抛物线y2=4x上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点P,则称弦AB是点P的一条“相关弦”。已知当x...