返回

高中一年级数学

首页
首页 高中一年级数学知识 任意角的三角函数 函数y=Asin（wx+φ）的图象与性质 试题正文
  • 解答题
    已知函数f（x）=2sinxcosx+2cos2x﹣1（x∈R）
    （Ⅰ）求函数f（x）的最小正周期及在区间[0，]上的最大值和最小值；
    （Ⅱ）若f（x0）=，x0∈[，]，求cos2x0的值．
    本题信息：2011年江西省月考题数学解答题难度较难 来源:沈诺（高中数学）
  • 本题答案
    查看答案
本试题 “已知函数f（x）=2sinxcosx+2cos2x﹣1（x∈R）（Ⅰ）求函数f（x）的最小正周期及在区间[0，]上的最大值和最小值；（Ⅱ）若f（x0）=，x0∈[，]，求cos2x0的值．” 主要考查您对

任意角的三角函数

函数y=Asin（wx+φ）的图象与性质

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 任意角的三角函数
  • 函数y=Asin（wx+φ）的图象与性质

任意角的三角函数的定义：

设α是任意一个角，α的终边上任意一点P的坐标是（x，y），它与原点的距离是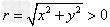，那么，，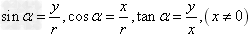
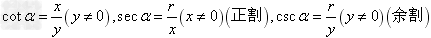以上以角为自变量，比值为函数的六个函数统称为三角函数。三角函数值只与角的大小有关，而与终边上点P的位置无关。

象限角的三角函数符号：

一全正，二正弦，三两切，四余弦。


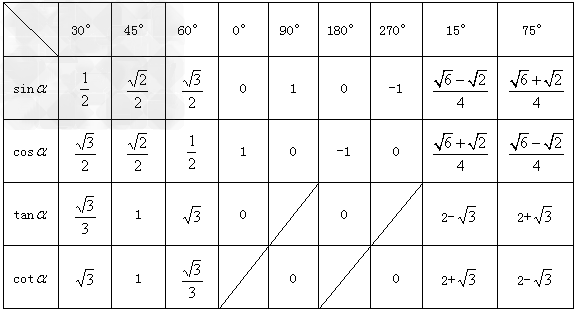
特殊角的三角函数值：（见下表）



函数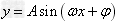的图象：

1、振幅、周期、频率、相位、初相：函数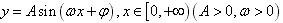，表示一个振动量时，A表示这个振动的振幅，往返一次所需的时间T=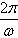，称为这个振动的周期，
单位时间内往返振动的次数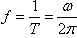称为振动的频率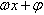，称为相位，x＝0时的相位叫初相。
2、用“五点法”作函数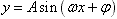的简图主要通过变量代换，设X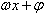＝由X取0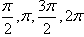，来找出相应的x的值，通过列表，计算得出五点的坐标，描点后得出图象。
3、函数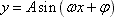＋K的图象与y=sinx的图象的关系：
把y=sinx的图象纵坐标不变，横坐标向左（φ＞0）或向右（φ＜0），y=sin（x+φ）
把y=sin（x+φ）的图象纵坐标不变，横坐标变为原来的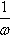，y=sin（ωx+φ）
把y=sin（ωx+φ）的图象横坐标不变，纵坐标变为原来的A倍，y=Asin（x+φ）
把y=Asin（x+φ）的图象横坐标不变，纵坐标向上（k＞0）或向下（k＜0），y=Asin（x+φ）+K；
若由y=sin（ωx）得到y=sin（ωx+φ）的图象，则向左或向右平移个单位。


函数y=Asin（x+φ）的性质：

1、y=Asin（x+φ）的周期为；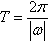
2、y=Asin（x+φ）的的对称轴方程是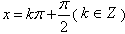，对称中心（kπ，0）。


发现相似题
与“已知函数f（x）=2sinxcosx+2cos2x﹣1（x∈R）（Ⅰ）求函数f（x...”考查相似的试题有：