本试题 “给出下列结论①函数f(x)=sin(2x+π2)是奇函数;②某小礼堂有25排座位,每排20个,一次心理学讲座,礼堂中坐满了学生,会后为了了解有关情况,留下座位号是15...” 主要考查您对真命题、假命题
正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
系统抽样
标准差、方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 真命题、假命题
- 正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
- 系统抽样
- 标准差、方差
命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
正弦函数和余弦函数的图象:正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的图象分别叫做正弦曲线和余弦曲线,
1.正弦函数 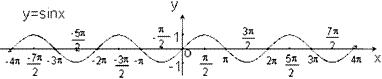
2.余弦函数
函数图像的性质
正弦、余弦函数图象的性质: 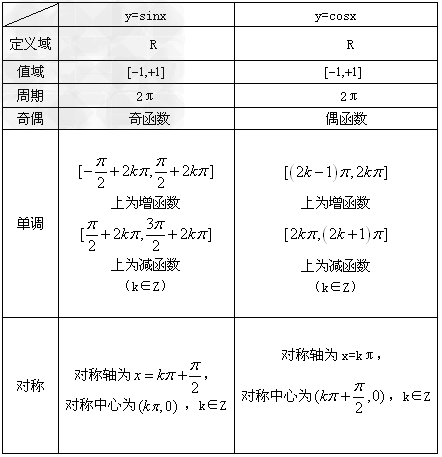
由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当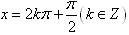 时,y取最大值1,
时,y取最大值1,
当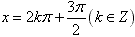 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
正弦、余弦函数图象的性质:

由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当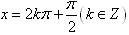 时,y取最大值1,
时,y取最大值1,
当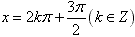 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
系统抽样的概念:
当整体中个体数较多时,将整体均分为几个部分,然后按一定的规则,从每一个部分抽取1个个体而得到所需要的样本的方法叫系统抽样。
系统抽样的步骤:
(1)采用随机方式将总体中的个体编号;
(2)将整个编号进行均匀分段在确定相邻间隔k后,若不能均匀分段,即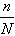 =k不是整数时,可采用随机方法从总体中剔除一些个体,使总体中剩余的个体数N′满足
=k不是整数时,可采用随机方法从总体中剔除一些个体,使总体中剩余的个体数N′满足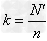 是整数;
是整数;
(3)在第一段中采用简单随机抽样方法确定第一个被抽得的个体编号l;
(4)依次将l加上ik,i=1,2,…,(n-1),得到其余被抽取的个体的编号,从而得到整个样本。
方差和标准差的定义:
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
设一组数据 的平均数为
的平均数为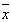 ,则
,则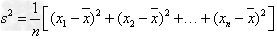 ,其中s2表示方差,s表示标准差。
,其中s2表示方差,s表示标准差。
一般地,平均数、方差、标准差具有如下性质:
若数据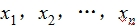 的平均数是
的平均数是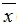 ,方差为s2,标准差为s.则新数据
,方差为s2,标准差为s.则新数据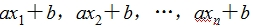 的平均数是a
的平均数是a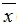 +b,方差为
+b,方差为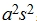 ,标准差为
,标准差为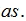
特别地,如a=1,则新数据的方差、标准差与原数据相同,分别为s2,s。因此,当一组数据均较大且接近某个常数时,可先将每个数同时减去这个常数,再计算这组新数据的方差,它与原数据的方差相等.
方差和标准差的意义:
方差和标准差都是用来描述一组数据波动情况的特征数,常数来比较两组数据的波动大小,方差较大的波动较大,方差较小的波动较小。
用样本的数字特征估计总体的数字特征分两类:
①用样本平均数估计总体平均数.
②用样本方差、标准差估计总体方差、标准差.样本容量越大,估计就越精确.
计算标准差的算法:
(1)算出样本数据的平均数;
(2)算出每个样本数据与样本平均数的差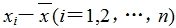 ;
;
(3)算出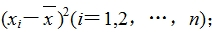
(4)算出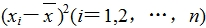 这n个数的平均数,即为样本方差s2;
这n个数的平均数,即为样本方差s2;
(5)算出方差的算术平方根,即为样本标准差s.
与“给出下列结论①函数f(x)=sin(2x+π2)是奇函数;②某小礼堂有...”考查相似的试题有:
- 给出下列四个命题:①函数y=|x|与函数y=(x)2表示同一个函数;②奇函数的图象一定通过直角坐标系的原点;③函数y=3(x-1)2的图象...
- 已知函数的图象与x轴的两个相邻交点的距离等于,若将函数的图象向左平移个单位长度得到函数的图象,则的解析式是( )A.B.C...
- 已知函数f(x)=(2cos2x-1)sin 2x+cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈,且f(α)=,求α的值.
- 已知函数f(x)=2sin2(π4+x)-3cos2x,x∈[π4,π2].(Ⅰ)求f(x)的最大值和最小值;(Ⅱ)若不等式|f(x)-m|<2在定义域上恒成...
- 已知是方程的两个根,则下列结论恒成立的是( )A.B.C.D.
- 函数的一条对称轴方程是( ).A.B.C.D.
- 已知函数.(Ⅰ)求的最小正周期;(Ⅱ)若函数的图象是由的图象向右平移个单位长度,再向上平移1个单位长度得到的,当[,]时,求...
- 将函数y=sinx•cosx的图象向右平移φ(φ>0)个单位后,得到的图象关于直线x=π6对称,则φ的最小值为( )A.5π12B.11π6C.11π1...
- y=tan(sin)的值域是A [,] B [,] C [tan1 ,tan1] D [-1 ,1]
- 若x1,x2,x3,…,x2009的方差为3,则3(x1-2),3(x2-2),3(x3-2),…,3(x2009-2)的方差为( ) A.3 B.9 C.18 D.27