本试题 “设A是三角形的内角,且sinA和cosA是关于x方程25x2-5ax-12a=0的两个根.(1)求a的值;(2)求tanA的值.” 主要考查您对函数的零点与方程根的联系
同角三角函数的基本关系式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的零点与方程根的联系
- 同角三角函数的基本关系式
函数零点的定义:
一般地,如果函数y =f(x)在实数a处的值等于零,即f(a)=o,则a叫做这个函数的零点,有时我们把一个函数的图象与x轴的交点的横坐标,也叫做这个函数的零点。
函数零点具有的性质:
对于任意函数y=(x)只要它的图象是连续不间断的,则有:
(1)当它通过零点时(不是二重零点),函数值变号.如函数f(x)=x2-2x -3的图象在零点-1的左边时,函数值取正号,当它通过第一个零点-1时,函数值由正变为负,在通过第二个零点3时,函数值又由负变为正.
(2)在相邻两个零点之间所有的函数值保持同号,
方程的根与函数的零点的联系:
方程f(x)=0有实根 函数y=f(x)的图像与x轴有交点
函数y=f(x)的图像与x轴有交点 函数y=f(x)有零点
函数y=f(x)有零点
同角三角函数的关系式:
(1)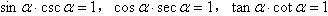 ;
;
(2)商数关系: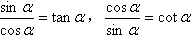 ;
;
(3)平方关系: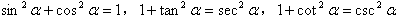 。
。
同角三角函数的基本关系的应用:
已知一个角的一种三角函数值,根据角的终边的位置利用同角三角函数的基本关系,可以求出这个角的其他三角函数值.
同角三角函数的基本关系的理解:
(1)在公式中,要求是同一个角,如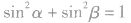 不一定成立.
不一定成立.
(2)上面的关系式都是对使它的两边具有意义的那些角而言的,如:基本三角关系式 。对一切α∈R成立;
。对一切α∈R成立;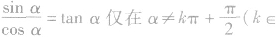 Z)时成立.
Z)时成立.
(3)同角三角函数的基本关系的应用极为为广泛,它们还有如下等价形式: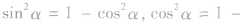

(4)在应用平方关系时,常用到平方根、算术平方根和绝对值的概念,应注意“±”的选取.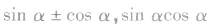 间的基本变形 三者通过
间的基本变形 三者通过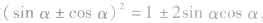 ,可知一求二,有关
,可知一求二,有关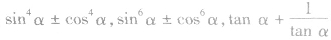 等化简都与此基本变形有广泛的联系,要熟练掌握。
等化简都与此基本变形有广泛的联系,要熟练掌握。
发现相似题
与“设A是三角形的内角,且sinA和cosA是关于x方程25x2-5ax-12a=0...”考查相似的试题有:
- 已知二次函数y=n(n+1)x2-(2n+1)x+1,当n依次取1,2,3,4,…10时,其图象在x轴上所截得的线段的长度的总和为( )A.1B....
- 已知函数f(x)x+1x,x>0x3+3,x≤0,则方程f(2x2+x)=a(a>2)的根的个数可能为______(将正确命题的序号全部填入)①1个②2...
- 若关于x的方程x2-mx+4=0在[-1,1]有解,则实数m的取值范围是______.
- 定义在R上的奇函数f(x),当时,,则函数的所有零点之和为( )A.B.C.D.
- ( )A.B.C.D.
- 已知sinα=45,π2<α<π,则tanα2的值为( )A.-12B.-2C.2D.12
- 已知角的终边过点,则( )A.B.C.D.
- (文科)已知α∈(π2,π),sinα=35,则tan(α+π4)=______.
- 在△ABC中,A,B,C所对的边分别为a,b,c,已知cosA=35,tanB2+cotB2=265,c=9(1)求tanB的值;(2)求△ABC的面积.
- 已知,求下列各式的值:(1); (2).