本试题 “下列说法错误的是[ ]A.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”B.“x=1”是“x2-3x+2=0”的充分不必要条件C.若p∧q为假命题,则p、q均为假...” 主要考查您对四种命题及其相互关系
充分条件与必要条件
简单的逻辑联结词
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 四种命题及其相互关系
- 充分条件与必要条件
- 简单的逻辑联结词
1、四种命题:
一般地,用p和q分别表示原命题的条件和结论,用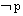 或
或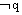 分别表示p和q的否定,
分别表示p和q的否定,
四种命题的形式是:
(1)原命题:若p则q;
(2)逆命题:若q则p;
(3)否命题:若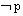 则
则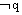 ;
;
(4)逆否命题:若 则
则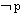 。
。
2、四种命题的真假关系:
一个命题与它的逆否命题是等价的,其逆命题与它的否命题也是等价的;
3、四种命题的相互关系:
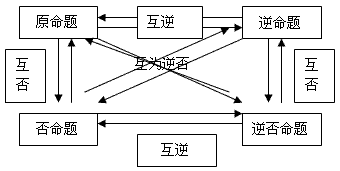
注意:
1、区别“否命题”与“命题的否定”,若原命题是“若p则q”,则这个命题的否定是“若p则非q”,而它的否命题是“若非p则非q”。
2、互为逆否命题同真假,即“等价”
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有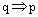 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且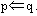 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
1、逻辑联结词:或、且、非;
2、且:一般地,用连接词“且”把命题p和命题q联结起来,得到一个新命题,记作p∧q,读作p且q;
3、或:一般地,用连接词“或”把命题p和命题q联结起来,得到一个新命题,记作p∨q,读作p或q;
4、非:一般地,对一个命题p全盘否定,就得到一个新命题,记作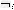 p,读作“非p”或“p的否定”;
p,读作“非p”或“p的否定”;
5、简单命题:不含逻辑联结词的命题(常用小写字母p,q,r,s,…表示)
6、复合命题:由简单命题和逻辑联结词构成的命题;
7、复合命题的形式及真值表:(1)“非p”的复合命题的真假与命题“p”的真假相反。
(2)“p且q”形式的复合命题的真假,只有命题“p”与“q”都为真时才为真,否则为假;
(3)“p或q”形式的复合命题的真假,只有命题“p”与“q”都为假时才为假,否则为真。
与“下列说法错误的是[ ]A.命题“若x2-3x+2=0,则x=1”的逆否命题...”考查相似的试题有:
- 下列命题正确的个数是( )①“在三角形ABC中,若,则”的逆命题是真命题;②命题或,命题则是的必要不充分条件;③“”的否定是“”;④...
- 命题“若a>b,则2a>2b”的否命题为( )A.若a>b,则有2a≤2b.B.若a≤b,则有2a≤2b.C.若a≤b,则有2a>2b.D.若2a≤2b,则有a...
- 已知原命题:设a、b是实数,若a+b≤0,则a≤0或b≤0.写出逆命题、否命题、逆否命题,并判断上述四个命题的真假.
- 设a∈R,则“a=1”是“直线l1:ax+2y=0与直线l2:x+(a+1)y+4=0平行”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件...
- 命题“a+b=2”是“直线x+y=0与圆(x-a)2+(y-b)2=2相切”的______条件.
- 若α:A={x|1<x<2},β:B{x|0≤x≤2},则α是β的( )条件
- “a=2”是“直线ax+2y=0平行于直线x+y=1”的[ ]A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
- 若Z1,Z2为复数,则Z12+Z22=0是Z1=0且Z2=0的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件
- 已知a,b为实数,则“a+b≤2”是“a≤1且b≤1”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 设集合A={x|-2