本试题 “已知函数f(x)=|x+1|,g(x)=2|x|+a,(Ⅰ)当a=0时,解不等式f(x)≥g(x);(Ⅱ)若存在x∈R,使得f(x)≥g(x)成立,求实数a的取值范围。” 主要考查您对分段函数与抽象函数
绝对值不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 分段函数与抽象函数
- 绝对值不等式
分段函数:
1、分段函数:定义域中各段的x与y的对应法则不同,函数式是分两段或几段给出的;
分段函数是一个函数,定义域、值域都是各段的并集。
抽象函数:
我们把没有给出具体解析式的函数称为抽象函数;
一般形式为y=f(x),或许还附有定义域、值域等,如:y=f(x),(x>0,y>0)。
知识点拨:
1、绝对值函数去掉绝对符号后就是分段函数。
2、分段函数中的问题一般是求解析式、反函数、值域或最值,讨论奇偶性单调性等。
3、分段函数的处理方法:分段函数分段研究。
绝对值不等式:
当a>0时,有 ;
;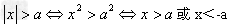 或x<-a 。
或x<-a 。
绝对值不等式的解法:
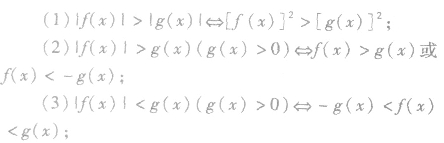
(4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解,也可以用图象法求解。
发现相似题
与“已知函数f(x)=|x+1|,g(x)=2|x|+a,(Ⅰ)当a=0时,解不等...”考查相似的试题有:
- 已知函数f(x)=-x-1(x<-2)x+3(-2≤x≤12)5x+1(x>12)(x∈R),(Ⅰ)求函数f(x)的最小值;(Ⅱ)已知m∈R,命题p:关于x的不等式...
- 设函数f(x)=x2+|x-2|-1,x∈R,(Ⅰ)判断函数f(x)的奇偶性;(Ⅱ)求函数f(x)的最小值。
- 已知函数f(x)=,则f(x)是[ ]A.非奇非偶函数,且在(0,+∞)上单调递增B.奇函数,且在R上单调递增C.非奇非偶函数,且在...
- (本题满分13分)已知函数.(Ⅰ)作出函数y=f(x)的图像:(Ⅱ)解不等式.
- 定义在R上的函数f(x)满足f(-x)=-f(x),f(x)=-f(x+2),且x∈(-1,0)时,f(x)=2x+15,则f(log220)=______.
- 已知函数f(x)=x+1(x≤1)-x+3(x>1),则f[f(52)]=______.
- 已知函数f(x)=x-3 x≥100f(x+5),x<100,则f(89)=______.
- 已知an=2n-1n+1(2+1n)m1≤n≤100 n>101(正整数m为常数),则limn→∞an=______.
- 已知f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e]时,f(x)=ax+lnx。(1)求f(x)的解析式;(2)是否存在负实...
- 若不等式|x-4|+|x-3|<a在R上的解集非空,则实数a的取值范围是______.