本试题 “已知函数f(x)=2x,等差数列{ax}的公差为2,若f(a2+a4+a6+a8+a10)=4,则log2[f(a1)·f(a2)·f(a3)·…·f(a10)]=( )。” 主要考查您对对数与对数运算
等差数列的定义及性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数与对数运算
- 等差数列的定义及性质
对数的定义:
如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记做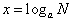 ,其中a叫做对数的底数,N叫做真数。
,其中a叫做对数的底数,N叫做真数。
通常以10为底的对数叫做常用对数,记做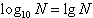 ;
;
以无理数e=2.71828…为底的对数叫做自然对数,记做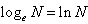 。
。
由定义知负数和0没有对数。
常用对数:
以10为底的对数叫做常用对数, 。
。
自然对数:
以e为底的对数叫做自然对数,e是无理数,e≈-2. 718 28, 。
。
对数的运算性质:
如果a>0,且a≠1,M>0,N>0,那么
(1)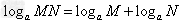 ;
;
(2)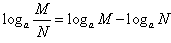 ;
;
(3) ;
;
(4) 。
。
对数的恒等式:
(1)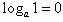 ;(2)
;(2)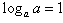 ;
;
(3)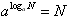 ;(4)
;(4) ;
;
(5)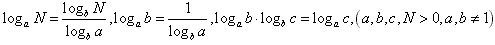 。
。
对数的换底公式及其推论:
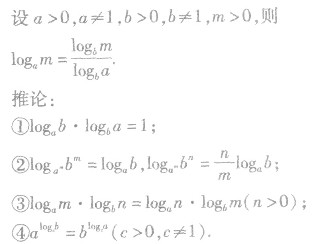
对数式的化简与求值:
(1)化同底是对数式变形的首选方向,其中经常用到换底公式及其推论.
(2)结合对数定义,适时进行对数式与指数式的互化.
(3)利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化,
等差数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做公差,用符号语言表示为an+1-an=d。
等差数列的性质:
(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;
(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;
(3)m,n∈N*,则am=an+(m-n)d;
(4)若s,t,p,q∈N*,且s+t=p+q,则as+at=ap+aq,其中as,at,ap,aq是数列中的项,特别地,当s+t=2p时,有as+at=2ap;
(5)若数列{an},{bn}均是等差数列,则数列{man+kbn}仍为等差数列,其中m,k均为常数。
(6)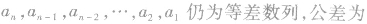
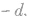
(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即

(8)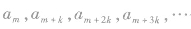 仍为等差数列,公差为
仍为等差数列,公差为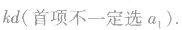
对等差数列定义的理解:
①如果一个数列不是从第2项起,而是从第3项或某一项起,每一项与它前一项的差是同一个常数,那么此数列不是等差数列,但可以说从第2项或某项开始是等差数列.
②求公差d时,因为d是这个数列的后一项与前一项的差,故有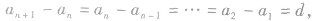 还有
还有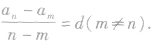
③公差d∈R,当d=0时,数列为常数列(也是等差数列);当d>0时,数列为递增数列;当d<0时,数列为递减数列;
④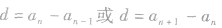 是证明或判断一个数列是否为等差数列的依据;
是证明或判断一个数列是否为等差数列的依据;
⑤证明一个数列是等差数列,只需证明an+1-an是一个与n无关的常数即可。
等差数列求解与证明的基本方法:
(1)学会运用函数与方程思想解题;
(2)抓住首项与公差是解决等差数列问题的关键;
(3)等差数列的通项公式、前n项和公式涉及五个量:a1,d,n,an,Sn,知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’).
与“已知函数f(x)=2x,等差数列{ax}的公差为2,若f(a2+a4+a6+a...”考查相似的试题有:
- 计算(log43+log83)(log32+log92)的值.
- 如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径...
- (本小题满分13分)已知等差数列的公差为,前项和为,且满足,(1)试用表示不等式组,并在给定的坐标系中画出不等式组表示的...
- 数列的首项为, 为等差数列且 .若则,,则( )A.0B.3C.8D.11
- 若是等差数列,首项,则使前n项和成的最大自然数n是: ( )A.4019B.4020C.4021D.4022
- 已知数列{an}中,a1=,an=2- (n≥2,n∈N*),数列{bn}满足bn=(n∈N*).(1)求证:数列{bn}是等差数列;(2)求数列{an}中的最大项和...
- 数列{an}是首项a1=4的等比数列,且S3,S2,S4成等差数列,(1)求数列{an}的通项公式;(2)若bn=log2|an|,设Tn为数列{1bnbn...
- 在△ABC中,三内角A、B、C成等差数列,则角B等于[ ]A.30°B.60°C.90°D.120°
- 已知x,f(x)2,3(x≥0)成等差数列.又数列an(an>0)中a1=3此数列的前n项的和Sn(n∈N+)对所有大于1的正整数n都有Sn=f(Sn-1...
- 在数列中,.从数列中选出项并按原顺序组成的新数列记为,并称为数列的项子列.例如数列、、、为的一个项子列.(1)试写出数列...