本试题 “若△ABC的对边分别为a、b、c且a=1,∠B=45°,S△ABC=2,则b=( )” 主要考查您对正弦定理
面积定理:S=1/2absinC=1/2acsinB=1/2bcsinA
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
- 面积定理:S=1/2absinC=1/2acsinB=1/2bcsinA
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即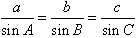 =2R。
=2R。
有以下一些变式:
(1)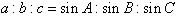 ;
;
(2)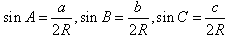 ;
;
(3)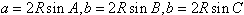 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 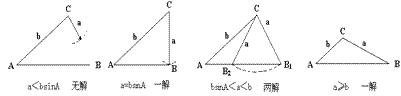
也可根据a,b的关系及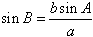 与1的大小关系来确定。
与1的大小关系来确定。
三角形面积公式:
(1)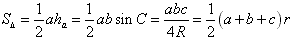
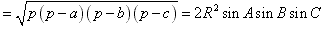 ,
,
其中r为三角形ABC内切圆半径,R为外接圆的半径, 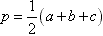 。
。
(2)数量积形式的三角形面积公式:
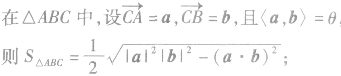
(3)坐标形式的三角形面积公式:

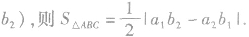
方法提炼:
(1)三角形的面积经常与正余弦定理结合在一起考查,解题时要注意方程思想的运用,即通过正余弦定理建立起方程(组),进而求得边或角;
(2)要熟记常用的面积公式及其变形.
发现相似题
与“若△ABC的对边分别为a、b、c且a=1,∠B=45°,S△ABC=2,则b=( )”考查相似的试题有:
- 在中,角的对边分别是,若成等差数列,的面积为,则 .
- 在锐角△ABC中,a,b,c分别为角A,B,C所对的边,且a=2csinA,角C=______.
- ΔABC中,若那么角B=___________
- 已知△ABC中,∠A=60°,a=6,b=4,那么满足条件的△ABC的形状大小( )A.有一种情形B.有两种情形C.不可求出D.有三种以上情形
- 在△ABC中,已知BC=5,sinC=2sinA,则AB=______.
- 在中,已知内角,边.设内角,面积为.(1)若,求边的长;(2)求的最大值.
- 在△ABC中,角A﹑B﹑C的对边分别是a,b,c,若a=5,cosA=-513,sinB=45.(Ⅰ)求b和sinC的值;(Ⅱ)求△ABC的面积.
- 已知△ABC中,a=1 , b=2,B=45°,则角A等于( )A.150°B.90°C.60°D.30°
- 在△ABC中,已知,则△ABC外接圆的半径的取值范围是[ ]A.[1,2]B.[1,]C.[,]D.[1,+∞)
- 在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=,(Ⅰ)求角C的大小;(Ⅱ)求sinA+sinB的最大值.