本试题 “如图,已知多面体ABCD﹣A1B1C1D1,它是由一个长方体ABCD﹣A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方...” 主要考查您对组合体的表面积与体积
直线与平面平行的判定与性质
直线与平面垂直的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 组合体的表面积与体积
- 直线与平面平行的判定与性质
- 直线与平面垂直的判定与性质
定义:
组合体的表面积与体积主要通过计算组成几何体的简单几何体的表面积与体积来求解。
组合体的表面积和体积与球有关的组合体问题:
一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图.如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或”、点。
求几何体的体积的几种常用方法:
(1)分割求和法:把不规则的图形分割成规则的图形,然后进行体积求和;
(2)补形法:把不规则形体补成规则形体,不熟悉形体补成熟悉形体,便于计算其体积;
常见的补形方法: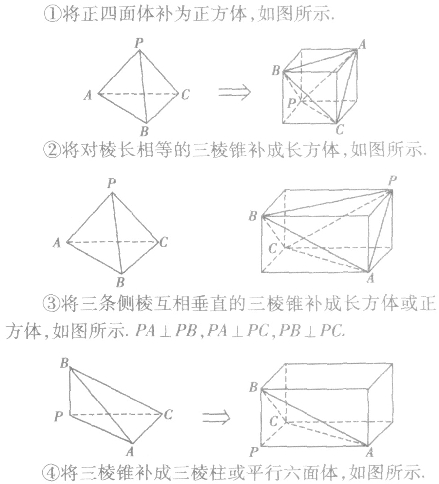
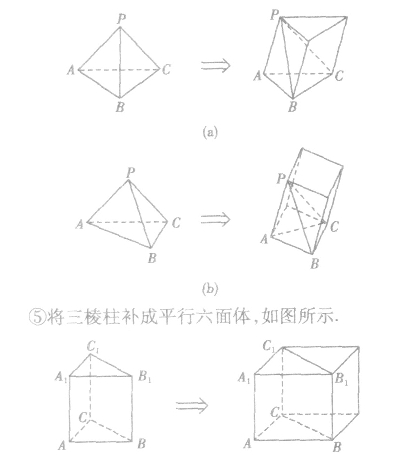
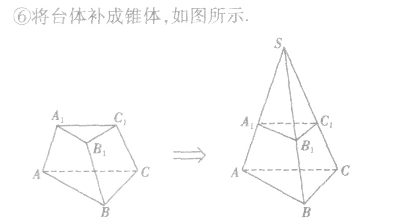
(3)等体积转化法:从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理,求原几何体的体积。
线面平行的定义:
若直线和平面无公共点,则称直线和平面平行。
线面平行的判定定理:
平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。 线线平行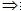 线面平行
线面平行
符号语言:
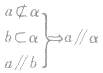
线面平行的性质定理:
如果一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。 线面平行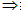 线线平行
线线平行
符号语言:
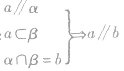
证明直线与平面平行的常用方法:
(l)反证法,即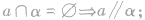
(2)判定定理法,即
(3)面面平行的性质定理,即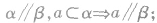
(4)向量法,平面外的直线 的方向向量n与平面
的方向向量n与平面 的法向量n垂直,则直线
的法向量n垂直,则直线 与平面
与平面 平行,即
平行,即
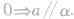
线面垂直的定义:
如果一条直线l和一个平面α内的任何一条直线垂直,就说这条直线l和这个平面α互相垂直,记作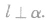 直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
线面垂直的画法:
画线面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示:
线面垂直的判定定理:
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。(线线垂直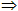 线面垂直)
线面垂直)
符号表示:
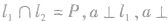
 如图所示,
如图所示,
线面垂直的性质定理:
如果两条直线同垂直于一个平面,那么这两条直线平行。
(线面垂直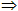 线线平行)
线线平行)
线面垂直的判定定理的理解:
(1)判定定理的条件中,“平面内的两条相交直线”是关键性语句,一定要记准.
(2)如果一条直线垂直于平面内的两条直线,那么这条直线垂直于这个平面,这个结论是错误的.
(3)如果一条直线垂直于平面内的无数条直线,那么这条直线垂直于这个平面,这个结论也错误,因为这无数条直线可能平行.
证明线面垂直的方法:
(1)线面垂直的定义拓展了线线垂直的范围,线垂直于面,线就垂直于面内所有直线,这也是线面垂直的必备条件,利用这个条件可将线线垂直与线面垂直互相转化,这样就完成了空间问题与平面问题的转化.
(2)证线面垂直的方法①利用定义:若一直线垂直于平面内任一直线,则这条直线垂直于该平面.②利用线面垂直的判定定理:证一直线与一平面内的两条相交直线都垂直,③利用线面垂直的性质:两平行线中的一条垂直于平面,则另一条也垂直于这个平面,④用面面垂直的性质定理:两平面垂直,在一个平面内垂直于交线的直线必垂直于另一个平面.⑤用面面平行的性质定理:一直线垂直于两平行平面中的一个,那么它必定垂直于另一个平面.⑥用面面垂直的性质:两相交平面同时垂直于第三个平面,那么两平面的交线垂直于第三个平面.⑦利用向量证明.
与“如图,已知多面体ABCD﹣A1B1C1D1,它是由一个长方体ABCD﹣A'B...”考查相似的试题有:
- 如果一空间几何体的正视图与侧视图均为等边三角形,俯视图是以半径为3的圆及其圆心,则这个几何体的体积为( )A.B.C.D.
- 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥SABC的体积为( )A.B.C.D.
- 如图是一个几何体的三视图,则这个几何体的体积是[ ]A.27B.30C.33D.36
- 设正方体的表面积为24,那么其外接球的体积是( )A. B.C. D.
- 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.①求证:A1F⊥面BEF;②求证:GC1∥面BEF...
- 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点,(Ⅰ)求证:A1D⊥平面BB1C1C;(Ⅱ...
- 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=23,O、H分别为AE、AB的中点.(1)求证:直线OH∥面BDE;(2...
- 如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.(Ⅰ)当PD∥平...
- 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.(1)求证:B1D1∥面A1BD;(2)求证:MD⊥AC;(3)...
- α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③m⊥β;④n⊥α,以其中三个论断作为条件...